题目内容
若函数f(x)满足f(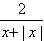 )=log2
)=log2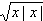 ,则f(x)的解析式是
,则f(x)的解析式是
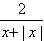 )=log2
)=log2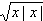 ,则f(x)的解析式是
,则f(x)的解析式是[ ]
A.f(x)=x-2
B.f(x)=2-x
C.f(x)=-log2x
D.f(x)=log2x
B.f(x)=2-x
C.f(x)=-log2x
D.f(x)=log2x
C

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
题目内容
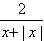 )=log2
)=log2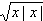 ,则f(x)的解析式是
,则f(x)的解析式是
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案