题目内容
在△ABC中，AB＝3，AC＝2，BC＝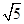
，则
等于 ( )
| A．2 | B．4 | C．3 | D．5 |
B
解析试题分析：：∵由余弦定理得
∴
故选D.
考点：平面向量数量积;余弦定理.
练习册系列答案
相关题目
设
为
的外心，且
，则的内角
=（ ）.
A． | B． | C． | D． |
设向量
满足
，
，则
（ ）
| A．1 | B．2 | C．3 | D．5 |
已知向量
，若函数
为偶函数，则
的值可能是（ ）
A． | B． | C． | D． |
已知向量
，
其中
，
，且
，则向量和的夹角是（ ）
A． | B． | C． | D． |
已知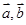
均为单位向量,它们的夹角为60°,那么
=（ ）
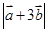A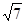． | B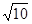． | C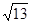． | D．4 |
若
，
，且
，则
与
的夹角是（ ）
A． | B． | C． | D． |
-
=1(a>0,b>0)上的点,F1,F2是其焦点,双曲线的离心率是
,且
·
=0,若△PF1F2的面积为9,则a+b的值为( )若向量
与
不共线，
，且
，则向量与
的夹角为 ( )
| A．0 |
B． |
C． |
D． |