题目内容
已知函数f(x)=log2(x2-ax-a)在区间(-∞,?1- ]上是单调递减函数.求实数a的取值范围.
]上是单调递减函数.求实数a的取值范围.
解:令g(x)=x2-ax-a,
则g(x)=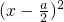 -a-
-a- ,由以上知g(x)的图象关于直线x=
,由以上知g(x)的图象关于直线x= 对称且此抛物线开口向上.
对称且此抛物线开口向上.
因为函数f(x)=log2g(x)的底数2>1,在区间(-∞,1- ]上是减函数,
]上是减函数,
所以g(x)=x2-ax-a在区间(-∞,1- ]上也是单调减函数,且g(x)≥0.
]上也是单调减函数,且g(x)≥0.
∴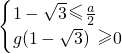 ,即
,即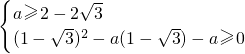 ,
,
∴解得2-2 ≤a≤2.
≤a≤2.
故a的取值范围是{a|2-2 ≤a≤2}.
≤a≤2}.
分析:先令g(x)=x2-ax-a,化为二次函数的顶点形式,根据复合函数的增减性判断方法得到g(x)为单调递减函数且根据对数定义得到g(x)>0,列出关于a的不等式求出解集即可.
点评:考查学生会求复合函数的单调区间的能力,以及理解函数恒成立的条件的能力.
则g(x)=
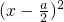 -a-
-a- ,由以上知g(x)的图象关于直线x=
,由以上知g(x)的图象关于直线x= 对称且此抛物线开口向上.
对称且此抛物线开口向上.因为函数f(x)=log2g(x)的底数2>1,在区间(-∞,1-
 ]上是减函数,
]上是减函数,所以g(x)=x2-ax-a在区间(-∞,1-
 ]上也是单调减函数,且g(x)≥0.
]上也是单调减函数,且g(x)≥0.∴
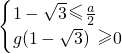 ,即
,即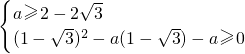 ,
,∴解得2-2
 ≤a≤2.
≤a≤2.故a的取值范围是{a|2-2
 ≤a≤2}.
≤a≤2}.分析:先令g(x)=x2-ax-a,化为二次函数的顶点形式,根据复合函数的增减性判断方法得到g(x)为单调递减函数且根据对数定义得到g(x)>0,列出关于a的不等式求出解集即可.
点评:考查学生会求复合函数的单调区间的能力,以及理解函数恒成立的条件的能力.

练习册系列答案
相关题目