题目内容
在△ABC中，cosA=
，cosB=
，b=3，则c=
或
或
．
| 3 |
| 5 |
| 5 |
| 13 |
| 14 |
| 5 |
| 4 |
| 5 |
| 14 |
| 5 |
| 4 |
| 5 |
分析：由cosA与cosB的值，利用同角三角函数间的基本关系求出sinA和sinB的值，再由b的长，利用正弦定理求出a的长，由a，b及cosA的值，利用余弦定理列出关于c的方程，求出方程的解即可得到c的长．
解答：解：∵在△ABC中，cosA=
，cosB=
，
∴sinA=
，sinB=
，又b=3，
∴由正弦定理
=
得：a=
=
=
，
∴由余弦定理a2=b2+c2-2bccosA，得：
=9+c2-
c，
解得：c=
或
．
故答案为：
或
| 3 |
| 5 |
| 5 |
| 13 |
∴sinA=
| 4 |
| 5 |
| 12 |
| 13 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| sinB |
3×
| ||
|
| 13 |
| 5 |
∴由余弦定理a2=b2+c2-2bccosA，得：
| 169 |
| 25 |
| 18 |
| 5 |
解得：c=
| 14 |
| 5 |
| 4 |
| 5 |
故答案为：
| 14 |
| 5 |
| 4 |
| 5 |
点评：此题考查了正弦、余弦定理，以及同角三角函数间的基本关系，熟练掌握正弦、余弦定理是解本题的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
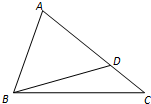如图，在△ABC中，cos∠ABC=