题目内容
在正方体ABCD—A1B1C1D1中，O1为BD的中点，O2为BC1的中点，O3为DC1的中点，求证：A1C⊥平面O1O2O3.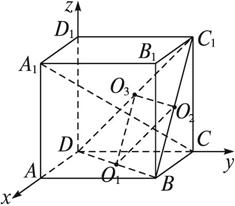
证明：不妨设正方体的棱长为1个单位长度，且设
.以i、j、k为坐标向量建立空间直角坐标系D—xyz,则C(0,1,0),A1(1,0,1),O1(
),O2(
),O3(0,
,
)，
=(-1,1,-1),
=(0,
,
),
=(-
,0,
).
∴
=-1×0+1×
+(-1)×
=0,
=-1×(-
)+1×0+(-1)·
=0.
∴
⊥
且
⊥
.
又∵O1O2∩O1O3=O1,∴A1C⊥平面O1O2O3.
绿色通道：
用向量坐标运算证明线线或线面垂直是向量的一个重要应用，要熟练掌握.关键是建系，求点的坐标，其中建系的恰当与否决定解题的繁简程度.
练习册系列答案
相关题目
16、在正方体ABCD-A′B′C′D′中，过对角线BD′的一个平面交AA′于E，交CC′于F，则
如图，在正方体ABCD-A′B′C′D′中，E，F分别是AB′，BC′的中点． 
如图在正方体ABCD-A 1B1C1D1中，O是底面ABCD的中心，B1H⊥D1O，H为垂足，则B1H与平面AD1C的位置关系是（ ）