题目内容
已知函数y=1-2a-2ax+2x2(-1≤x≤1)的最小值为f(a).
(Ⅰ)求f(a)的表达式;
(Ⅱ)当a∈[-2,0]时,求Q=log
f(a)的值域.
(Ⅰ)求f(a)的表达式;
(Ⅱ)当a∈[-2,0]时,求Q=log
| 1 |
| 3 |
(Ⅰ)有题意y=2(x-
)2-
-2a+1(-1≤x≤1),
当
<-1,即a<-2时,ymin=y|x=-1=f(a)=3;…(2分)
当-1≤
≤1,即-2≤a≤2时,ymin=y|x=
=f(a)=-
-2a+1;…(4分)
当
>1,即a>2时,ymin=y|x=1=f(a)=3-4a,…(6分)
∴f(a)=
a≤2.…(8分)
(Ⅱ)当a∈[-2,0]时,Q=log
f(a)=log
(-
-2a+1),
设u=-
-2a+1=-
(a+2)2+3,a∈[-2,0],则1≤u≤3,…(10分)
此时Q=log
u∈[-1,0].
∴Q=log
f(a)的值域为[-1,0].…(12分)
| a |
| 2 |
| a2 |
| 2 |
当
| a |
| 2 |
当-1≤
| a |
| 2 |
| a |
| 2 |
| a2 |
| 2 |
当
| a |
| 2 |
∴f(a)=
|
(Ⅱ)当a∈[-2,0]时,Q=log
| 1 |
| 3 |
| 1 |
| 3 |
| a2 |
| 2 |
设u=-
| a2 |
| 2 |
| 1 |
| 2 |
此时Q=log
| 1 |
| 3 |
∴Q=log
| 1 |
| 3 |

练习册系列答案
相关题目
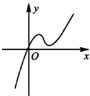 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若正数a,b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示.若正数a,b满足f(2a+b)<1,则 的值域.
的值域.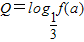 的值域.
的值域.