题目内容
设函数f(x)的导函数为f′(x),且f(x)=x2+2x•f′(1)+3,则f′(1)的值为( )
分析:求出原函数的导函数,在导函数解析式中取x=1即可得到答案.
解答:解:由f(x)=x2+2x•f′(1)+3,
得f′(x)=2x+2f′(1),
∴f′(1)=2+2f′(1),解得f′(1)=-2.
故选D.
得f′(x)=2x+2f′(1),
∴f′(1)=2+2f′(1),解得f′(1)=-2.
故选D.
点评:本题考查了导数的加法法则与减法法则,考查了基本初等函数的导函数,是基础的计算题.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
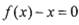 有实数根;
有实数根;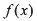 的导数
的导数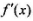 (满足
(满足 ”
” 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程 只有一个实根;
只有一个实根;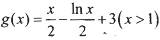 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;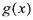 定义域内的任一区间
定义域内的任一区间 ,都存在
,都存在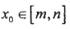 ,使得
,使得 ”,请利用函数
”,请利用函数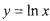 的图象说明这一结论.
的图象说明这一结论.