题目内容
如图所示,正方体 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:
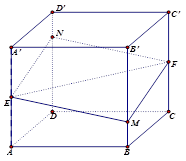
①平面
 平面
平面 ;
;
②当且仅当 时,四边形
时,四边形 的面积最小;
的面积最小;
③四边形 周长
周长 ,
, 是单调函数;
是单调函数;
④四棱锥 的体积
的体积 为常函数;
为常函数;
以上命题中真命题的序号为 。
 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:
①平面

 平面
平面 ;
;②当且仅当
 时,四边形
时,四边形 的面积最小;
的面积最小; ③四边形
 周长
周长 ,
, 是单调函数;
是单调函数;④四棱锥
 的体积
的体积 为常函数;
为常函数;以上命题中真命题的序号为 。
①②④
试题分析:①连结
 ,则由正方体的性质可知,
,则由正方体的性质可知, 平面
平面 ,所以平面
,所以平面 平面
平面 ,所以①正确;②连结
,所以①正确;②连结 ,因为
,因为 平面
平面 ,所以
,所以 ,四边形
,四边形 的对角线
的对角线 是固定的,所以要使面积最小,则只需
是固定的,所以要使面积最小,则只需 的长度最小即可,此时当
的长度最小即可,此时当 为棱的中点时,即
为棱的中点时,即 时,此时
时,此时 长度最小,对应四边形
长度最小,对应四边形 的面积最小.所以②正确;③因为
的面积最小.所以②正确;③因为 ,所以四边形
,所以四边形 是菱形.当
是菱形.当 时,
时, 的长度由大变小.当
的长度由大变小.当 时,
时, 的长度由小变大.所以函数
的长度由小变大.所以函数 不单调.所以③错误;④连结
不单调.所以③错误;④连结 则四棱锥分割为两个小三棱锥,它们以
则四棱锥分割为两个小三棱锥,它们以 为底,以
为底,以 分别为顶点的两个小棱锥.因为
分别为顶点的两个小棱锥.因为 的面积是个常数,
的面积是个常数, 到平面
到平面 的距离是个常数,所以四棱锥
的距离是个常数,所以四棱锥 的体积
的体积 为常函数,所以④正确.所以选C.
为常函数,所以④正确.所以选C.
练习册系列答案
相关题目
 ,
, ,DC=1,AB=2,PA⊥平面ABCD,PA=1.
,DC=1,AB=2,PA⊥平面ABCD,PA=1.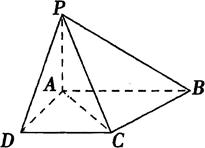
 ,BC = 6.
,BC = 6.
 中,四边形
中,四边形 是菱形,
是菱形,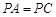 ,E为PB的中点.
,E为PB的中点.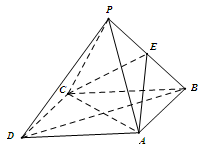
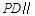 平面
平面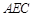 ;
;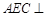 平面
平面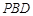 .
.  中,底面
中,底面 为菱形,其中
为菱形,其中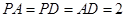 ,
, ,
, 为
为 的中点.
的中点.
 ;
; 平面
平面 为
为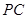 的中点,求四棱锥
的中点,求四棱锥 的体积.
的体积.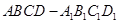 中,
中,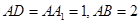 ,点E为AB的中点.
,点E为AB的中点.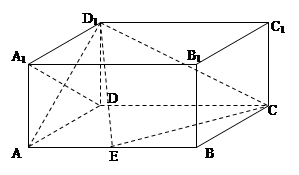
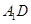 与平面
与平面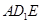 所成的角;
所成的角; 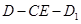 的平面角的正切值.
的平面角的正切值. 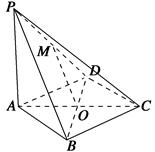
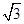 时,求PB的长.
时,求PB的长.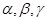 ,若
,若 ,则
,则 ∥
∥
 ,若
,若 ,直线
,直线 与
与 与
与 与棱长为
与棱长为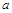 正四面体各面都相切,则该球的表面积为
正四面体各面都相切,则该球的表面积为 ;
; 中,
中, 则
则 .
.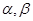 是两个互相垂直的平面,
是两个互相垂直的平面,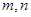 是一对异面直线,下列五个结论:
是一对异面直线,下列五个结论: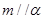 ,
,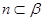 (2)
(2)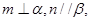 (3)
(3)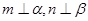
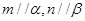 (5)
(5)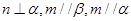 。其中能得到
。其中能得到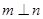 的结论有 (把所有满足条件的序号都填上)
的结论有 (把所有满足条件的序号都填上)