题目内容
(1)求函数f(x)=x3-x2-40x+80的单调区间;
(2)若函数y=x3+bx2+cx在区间(-∞,0)及[2,+∞]是增函数,而在(0,2)是减函数,求此函数在[-1,4]上的值域.
【答案】
(1)单调增区间 ;单调减区间
;单调减区间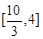
(2)b=-3,c=0;此函数在[-1,4]上的值域为[-4,16].
【解析】
试题分析:(1) ,
,
令 f '(x)=0 ,得  ,
,
当 x<  时,f '(x)>0 ;当
时,f '(x)>0 ;当  <x<4 时,f '(x)<0 ;当 x>4 时,f '(x)>0 ,
<x<4 时,f '(x)<0 ;当 x>4 时,f '(x)>0 ,
所以函数在(-∞, ] 上为增函数,在 [
] 上为增函数,在 [ ,4] 上为减函数,在 [4,+∞)上为增函数。
,4] 上为减函数,在 [4,+∞)上为增函数。
(2)因为y=x³+bx²+cx,在(-∞,0),[2,+∞)递增,(0,2)递减,
所以0和2分别是极大值点和极小值点,是方程y'=3x²+2bx+c=0的根。
c=0,3·2²+4b=0,b=-3,即y=x³-3x²
由f(0)=0,f(2)=-4,f(-1)=-1-3=-4,f(4)=16
∴y∈[-4,16]
考点:本题主要考查利用导数研究函数的单调性,求函数的极值。
点评:基本题型,以函数为载体,通过应用导数知识,对函数单调性、极值、不等式的解法等进行了全面考查。

练习册系列答案
相关题目
 设函数
设函数