题目内容
19.设随机变量X~N(10,1),P(9≤x<10)=a,其中a=$\int_{\frac{1}{9}}^{\frac{1}{4}}{\frac{1}{{\sqrt{x}}}dx}$,则P(X≥11)=$\frac{1}{6}$.分析 随机变量X~N(10,1),得到曲线关于X=10称,根据曲线的对称性得到P(X≥11)=P(X≤9)=0.5-P(9≤x<10),根据概率的性质得到结果.
解答 解:a=$\int_{\frac{1}{9}}^{\frac{1}{4}}{\frac{1}{{\sqrt{x}}}dx}$=2$\sqrt{x}$${|}_{\frac{1}{9}}^{\frac{1}{4}}$=$\frac{1}{3}$,
∴P(9≤x<10)=$\frac{1}{3}$.
∴随机变量X~N(10,1),
∴曲线关于X=10对称,
∴P(X≥11)=P(X≤9)=0.5-P(9≤x<10)=$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识,属于基础题.

练习册系列答案
相关题目
9.已知某高级中学高三学生有2000名,在第一次模拟考试中数学成绩ξ服从正态分布N(120,σ2),已知P(100<?<120)=0.45.若学校教研室欲按分层抽样的方式从中抽出100份试卷进行分析研究,则应从140分以上的试卷中抽( )
| A. | 4份 | B. | 5份 | C. | 8份 | D. | 10份 |
10.执行如图所示的程序框图,输出的S值为( )
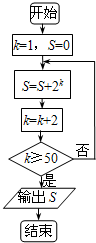

| A. | $\frac{2}{3}({4^{25}}-1)$ | B. | $\frac{2}{3}({4^{26}}-1)$ | C. | 250-1 | D. | 251-1 |
14.甲、乙两个养猪场每回出栏的成猪都在90~110公斤之间,重达102公斤的成猪称为优质猪.已知甲、乙两个养猪场每回养猪100头,本回出栏的成猪重量分布如下:
甲养猪场猪重频数分布表
乙养猪场猪重频数分布表
(Ⅰ)分别估计甲养猪场、乙养猪场出栏成猪的优质率;
(Ⅱ)已知乙养猪场出栏一头猪的利润y(单位:百元)与其重量x(单位:公斤)的关系为:y=$\left\{\begin{array}{l}{-2(x<94)}\\{2(94≤x<102)}\\{4(x≥102)}\end{array}\right.$估计乙养猪场平均每出栏一头猪的利润.
甲养猪场猪重频数分布表
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 8 | 20 | 42 | 22 | 8 |
| 猪的重量分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110) |
| 频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅱ)已知乙养猪场出栏一头猪的利润y(单位:百元)与其重量x(单位:公斤)的关系为:y=$\left\{\begin{array}{l}{-2(x<94)}\\{2(94≤x<102)}\\{4(x≥102)}\end{array}\right.$估计乙养猪场平均每出栏一头猪的利润.
8.若函数f(x)=$\frac{{2}^{x}+1}{{2}^{x}-a}$是奇函数,则使f(x)>3成立的x的取值范围为( )
| A. | (-∞,-1) | B. | (-1,0) | C. | (0,1) | D. | (1,+∞) |
9.设α,β是两个不同的平面,m是直线且m?α,“m∥β“是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |