题目内容
已知函数f(x)=2asin2x-2
解:f(x)=a(1-cos2x)-![]() asin2x+a+b
asin2x+a+b
=-a(cos2x+![]() sin2x)+
sin2x)+
=-2asin(2x+![]() )+
)+
∵x∈[0, ![]() ],∴2x+
],∴2x+![]() ∈[
∈[![]() ,
,![]() ],
],
∴-![]() ≤sin(2x+
≤sin(2x+![]() )≤1,
)≤1,
因此,由函数的值域是[-5,1],
可得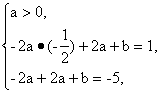 即
即![]()
或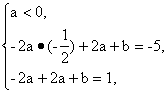 即
即![]()
综上所述,a,b的值为![]() 或
或![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
题目内容
已知函数f(x)=2asin2x-2
解:f(x)=a(1-cos2x)-![]() asin2x+a+b
asin2x+a+b
=-a(cos2x+![]() sin2x)+
sin2x)+
=-2asin(2x+![]() )+
)+
∵x∈[0, ![]() ],∴2x+
],∴2x+![]() ∈[
∈[![]() ,
,![]() ],
],
∴-![]() ≤sin(2x+
≤sin(2x+![]() )≤1,
)≤1,
因此,由函数的值域是[-5,1],
可得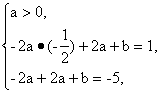 即
即![]()
或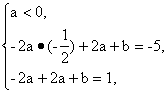 即
即![]()
综上所述,a,b的值为![]() 或
或![]()

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案