题目内容
设函数 的前n项和为
的前n项和为
- A.

- B.

- C.

- D.
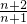
C
分析:对函数求导,然后结合f′(x)=2x+1,可求t,m,进而可求f(x),代入可得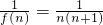 =
=
,利用裂项可求数列的和
解答:对函数求导可得f′(x)=mxm-1+t=2x+1
由题意可得,t=1,m=2
∴f(x)=x2+x=x(x+1)
∴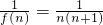 =
=
∴ =
=
=
故选C
点评:本题主要考查了函数的求导,裂项相消求解数列的和,体现了函数与数列的结合
分析:对函数求导,然后结合f′(x)=2x+1,可求t,m,进而可求f(x),代入可得
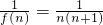 =
=
,利用裂项可求数列的和
解答:对函数求导可得f′(x)=mxm-1+t=2x+1
由题意可得,t=1,m=2
∴f(x)=x2+x=x(x+1)
∴
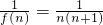 =
=
∴
 =
=
=

故选C
点评:本题主要考查了函数的求导,裂项相消求解数列的和,体现了函数与数列的结合

练习册系列答案
相关题目
 的前n项和为( )
的前n项和为( )



 的前n项和为( )
的前n项和为( )



 的前n项和为( )
的前n项和为( )


