Question

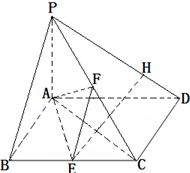如图，四棱锥P-ABCD的底面是菱形，∠ABC=60°，PA⊥底面ABCD，E、F分别是BC、PC的中点，PA=AB=2．
（1）若H为PD上的动点，求EH与平面PAD所成的最大角的正切值；
（2）求二面角E-AF-C的余弦值．

Answer 1

分析：（1）以AB所在直线为x轴，以AP所在直线为z轴，以过点A且与AB垂直的直线为y轴建立空间直角坐标系，可得

EH

=（λ-

5

2

，

3

2

-

3

λ，2λ），易得平面PAD的一个法向量为

AE

=（

3

2

，

3

2

，0），设直线EH与平面PAD所成的角的角为θ，计算可得sinθ=|cos＜

EH

，

AE

＞|=

3

8(λ- 1 2 )2+5

，当λ=

1

2

时，sinθ取得最大值为

3

5

，可得此时的正切的最值；
（2）可得

BD

=（-3，

3

，0）为平面AFC的法向量．又可求得

n

=（-1，

3

，-1）为平面AFE的法向量，可得法向量夹角的余弦值，可得结论．

解答：解：（1）以AB所在直线为x轴，以AP所在直线为z轴，以过点A且与AB垂直的直线为y轴建立空间直角坐标系，
由题意，A（0，0，0），B（2，0，0），C（1，

3

，0），从而E（

3

2

，

3

2

，0），D（-1，

3

，0），P（0，0，2），
设H（x，y，z），并设

DH

=λ

DP

，即（x+1，y-

3

，z）=λ（1，-

3

，2）
所以F（λ-1，

3

-

3

λ，2λ），所以

EH

=（λ-

5

2

，

3

2

-

3

λ，2λ），
由条件易证AE⊥平面PAD，所以平面PAD的一个法向量为

AE

=（

3

2

，

3

2

，0），
设直线EH与平面PAD所成的角的角为θ，则sinθ=|cos＜

EH

，

AE

＞|=|

EH • AE

| EH || AE |

|
=|

3 2 (λ- 5 2 )+ 3 2 ( 3 2 - 3 λ)

(λ- 5 2 )2+( 3 2 - 3 λ)2+4λ2 • 9 4 + 3 4

|=

3

8(λ- 1 2 )2+5

所以，当λ=

1

2

时，sinθ取得最大值为

3

5

，从而cosθ=

2

5

，此时，tanθ=

3

2

=

6

2

（2）由条件易证BD⊥平面AFC，故取

BD

=（-3，

3

，0）作平面AFC的法向量．
设平面AFE的法向量为

n

=（x，y，z），则

n

⊥

AF

且

n

⊥

AE

，
所以，

1 2 x+ 3 2 y+z=0 3 2 x+ 3 2 y=0

，取y=

3

，则x=-1，z=-1，
即

n

=（-1，

3

，-1），设二面角E-AF-C的平面角为θ，由图可知此二面角为锐二面角，
故cosθ=|cos＜

BD

，

n

＞|=|

BD • n

| BD || n |

|=|

3+3

12 5

|=

15

5

点评：本题考查向量法求解立体几何问题，转化为平面的法向量之间的夹角是夹角问题的关键，属中档题．