题目内容
（2012•青浦区一模）已知三棱柱ABC-A1B1C1的体积为30cm3，P为其侧棱BB1上的任意一点，则四棱锥P-A1C1CA的体积为
20
20
cm3．分析：四棱锥P-A1CC1A的体积=三棱柱ABC-A1B1C1的体积-三棱锥P-ABC体积-三棱锥P-A1B1C1后的体积，由此能求出四棱锥P-A1CC1A的体积．
解答：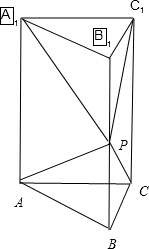
解：四棱锥P-A1C1CA的体积=三棱柱ABC-A1B1C1的体积-三棱锥P-ABC体积-三棱锥P-A1B1C1后的体积，
∵VP-ABC=
•S△ABC•B1P，
VP-A1B1C1=
•S△A1B1C1•B1P，
S△ABC=S△A1B1C1，
BP+B1P=BB1，
S△ABC×BB1=30，
∴四棱锥P-A1C1CA的体积V=VABC-A1B1C1-（VP-ABC+VP-A1B1C1）=30-30×
=20．
故答案为：20．
解：四棱锥P-A1C1CA的体积=三棱柱ABC-A1B1C1的体积-三棱锥P-ABC体积-三棱锥P-A1B1C1后的体积，∵VP-ABC=
| 1 |
| 3 |
VP-A1B1C1=
| 1 |
| 3 |
S△ABC=S△A1B1C1，
BP+B1P=BB1，
S△ABC×BB1=30，
∴四棱锥P-A1C1CA的体积V=VABC-A1B1C1-（VP-ABC+VP-A1B1C1）=30-30×
| 1 |
| 3 |
故答案为：20．
点评：本题考查棱锥的体积的计算，解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
阅读快车系列答案
相关题目
（2012•青浦区一模）定义某种新运算⊙：s=a⊙b的运算原理如图流程图所示，则5⊙4-3⊙4=
（2012•青浦区一模）如图：三棱锥P-ABC中，PA⊥底面ABC，若底面ABC是边长为2的正三角形，且PB与底面ABC所成的角为