题目内容
在△ABC中，
，则AC边上的高为
- A.
- B.
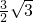
- C.1
- D.
A
分析：BD为高，那么题中有两个直角三角形，BD在这两个直角三角形中，设AD为未知数，可利用勾股定理都表示出BD长．求得AD长，再根据勾股定理求得BD长．
解答：设AD=x，则CD=3-x，在Rt△ABD中，BD2+x2=（
）2
在Rt△BDC中，BD2=22-（3-x）2
所以有（）2-x2=22-（3-x）2，解得x=2
在Rt△ABD中，BD=
．
故选A．
点评：解决本题的关键在于利用两个直角三角形的公共边找到突破点，主要利用了勾股定理进行解答，属于中档题．
分析：BD为高，那么题中有两个直角三角形，BD在这两个直角三角形中，设AD为未知数，可利用勾股定理都表示出BD长．求得AD长，再根据勾股定理求得BD长．
解答：设AD=x，则CD=3-x，在Rt△ABD中，BD2+x2=（
）2在Rt△BDC中，BD2=22-（3-x）2
所以有（
）2-x2=22-（3-x）2，解得x=2在Rt△ABD中，BD=
．故选A．
点评：解决本题的关键在于利用两个直角三角形的公共边找到突破点，主要利用了勾股定理进行解答，属于中档题．
练习册系列答案
53随堂测系列答案
相关题目
ABC中．
．则A的取值范围是 
] B．[ 
） C．（0，
] D．[ 
，则A的取值范围是 
B．
C．
D．
则
( ) 
B、
C、
D、
、
是第二象限角，则
；③三角形的内角是第一象限角或第二象限角；④函数
是最小正周期为
的周期函数；⑤在△ABC中，若
,则A>B.其中正确的是___________ （写出所有正确说法的序号） 
是第二象限角，则
；③三角形的内角是第一象限角或第二象限角；④函数
是最小正周期为
的周期函数；⑤在△ABC中，若
,则A>B.其中正确的是_________. （写出所有正确说法的序号）