Question

已知椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）和双曲线

x2

m2

-

y2

n2

=1（m＞0，n＞0）有公共的焦点F₁，F₂，P是两曲线的一个交点．求证：
（1）|PF1|•|PF2|=a2-m2
（2）S_△F1PF2=bn
（3）tan

∠F1PF2

2

=

n

b

．

Answer 1

分析：（1）先根据点P为椭圆和双曲线的一个交点结合定义求出|PF₁|与|PF₂|的表达式，代入即可求出|PF₁|•|PF₂|的值．
（2）利用（1）中得出的结论，结合三角形面积公式即可证得．
（3）利用三角函数中正切的半角公式，结合前面得出的结论，即可证得．

解答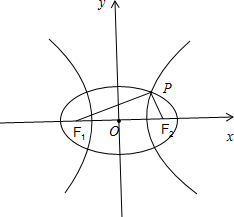：解：（1）不妨设P在双曲线的右支上，左、右焦点F₁、F₂．利用椭圆以及双曲线的定义可得：|PF₁|+|PF₂|=2a   ①
|PF₁|-|PF₂|=2m    ②
由①②得：|PF₁|=a+m，|PF₂|=a-m．
∴|PF₁|•|PF₂|=a²-m²．
（2）如图所示，因为椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）和双曲线

x2

m2

-

y2

n2

=1（m＞0，n＞0）有公共的焦点F₁、F₂，
所以有：a²-b²=m²+n²，
不妨设两曲线的交点P位于双曲线的右支上，设|PF₁|=p，|PF₂|=q．
由双曲线和椭圆的定义可得 p+q=2a，p-q=2m，
解得 p²+q²=2（a²+m²），pq=a²-m²，
在△PF₁F₂中，cos∠F₁PF₂=

p2+q2-4c2

2pq

=

b2-n2

2(a2-m2)

．
∴S_△F1PF2=

1

2

pqsin∠F₁PF₂=

1

2

×（a²-m²）×

1-cos2∠F1PF2

=bn．
（3）tan

∠F1PF2

2

=

1-cos∠F1PF2

sin∠F1PF2

=

1- b2-n2 2(a2-m2)

1-cos2∠F1PF2

=

1- b2-n2 2(a2-m2)

1-( b2-n2 2(a2-m2) )2

=

n

b

．

点评：本题主要考查圆锥曲线的综合问题．解决本题的关键在于根据椭圆和双曲线有相同的焦点F₁、F₂，及圆锥曲线的定义．属于中档题．