题目内容
把下列集合用另一种方法表示出来:(1){x|x2-x-6=0};
(2){y|y=x2-x-6,x∈R};
(3){(x,y)|y=x2-x-6,x∈R};
(4){x|y=x2-x-6}.
思路分析:(1)代表元素为x,x满足的条件是x2-x-6=0,因此这个集合是方程x2-x-6=0的解集,所以这个集合还可表示为{-2,3}.
(2)代表元素是y,这个集合是当x取任意实数时,二次函数y=x2-x-6的所有函数值的集合.而y=x2-x-6=(x-![]() )2-
)2-![]() ,故函数y=x2-x-6有最小值-
,故函数y=x2-x-6有最小值-![]() ,无最大值.所以这个集合还可表示为{y|y≥-
,无最大值.所以这个集合还可表示为{y|y≥-![]() }.
}.
(3)代表元素是(x,y),是直角坐标系中点的坐标形式,并且满足y=x2-x-6,因此这个集合是由抛物线y=x2-x-6上所有点构成的点的集合(点集).所以这个集合还可以表示为{抛物线y=x2-x-6上的点}.
(4)代表元素是x,x是函数y=x2-x-6的自变量,因此这个集合是函数y=x2-x-6的自变量的取值集合.所以这个集合为{x|x∈R},即为R.
答案:(1){-2,3}.
(2){y|y≥-![]() }.
}.
(3){抛物线y=x2-x-6上的点}.
(4)R.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
把下列集合用另一种方法表示出来.
|
(1){4 ,5,6,7,8} |
(2){1 ,3,5,7} |
|
(3) |
(4) |




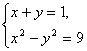 的解集.
的解集.