题目内容
设Sn是各项均为非零实数的数列{an}的前n项和,给出如下两个命题上:命题p:{an}是等差数列;命题q:等式
+
+…+
=
对任意n(n∈N*)恒成立,其中k,b是常数.
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件
+
≤M,试求Sn的最大值.
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| kn+b |
| a1an+1 |
(1)若p是q的充分条件,求k,b的值;
(2)对于(1)中的k与b,问p是否为q的必要条件,请说明理由;
(3)若p为真命题,对于给定的正整数n(n>1)和正数M,数列{an}满足条件
| a | 21 |
| a | 2n+1 |
(1)设{an}的公差为d,则原等式可化为
(
-
+
-
+…+
-
)=
,
所以
•
=
,
即(k-1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…(4分)
(2)当k=1,b=0时,假设p是q的必要条件,即“若
+
+…+
=
①对于任意的n(n∈N*)恒成立,则{an}为等差数列”.
当n=1时,
=
显然成立.…(6分)
当n≥2时,若
+
+…+
=
②,
由①-②得,
=
(
-
),即nan-(n-1)an+1=a1③.
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n-1)an-1-(n-2)an=a1④,即2an=an-1+an+1.所以{an}为等差数列,即p是q的必要条件.…(10分)
(3)由
+
≤M,可设a1=rcosθ,an+1=rsinθ,所以r≤
.
设{an}的公差为d,则an+1-a1=nd=rsinθ-rcosθ,
所以d=
,
所以an=rsinθ-
,
Sn=
=
r≤
•
=
,
所以Sn的最大值为
…(16分)
| 1 |
| d |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an |
| 1 |
| an+1 |
| kn+b |
| a1an+1 |
所以
| 1 |
| d |
| nd |
| a1an+1 |
| kn+b |
| a1an+1 |
即(k-1)n+b=0对于n∈N*恒成立,所以k=1,b=0.…(4分)
(2)当k=1,b=0时,假设p是q的必要条件,即“若
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| anan+1 |
| n |
| a1an+1 |
当n=1时,
| 1 |
| a1a2 |
| 1 |
| a1a2 |
当n≥2时,若
| 1 |
| a1a2 |
| 1 |
| a2a3 |
| 1 |
| an-1an |
| n-1 |
| a1an+1 |
由①-②得,
| 1 |
| anan+1 |
| 1 |
| a1 |
| n |
| an+1 |
| n-1 |
| an |
当n=2时,a1+a3=2a2,即a1、a2、a3成等差数列,
当n≥3时,(n-1)an-1-(n-2)an=a1④,即2an=an-1+an+1.所以{an}为等差数列,即p是q的必要条件.…(10分)
(3)由
| a | 21 |
| a | 2n+1 |
| M |
设{an}的公差为d,则an+1-a1=nd=rsinθ-rcosθ,
所以d=
| rsinθ-rcosθ |
| n |
所以an=rsinθ-
| rsinθ-rcosθ |
| n |
Sn=
| (a1+an)n |
| 2 |
| (n+1)cosθ+(n-1)sinθ |
| 2 |
| ||
| 2 |
| M |
| ||
| 2 |
| M(n2+1) |
所以Sn的最大值为
| ||
| 2 |
| M(n2+1) |

练习册系列答案
相关题目
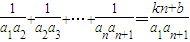 对任意n(n∈N*)恒成立,其中k,b是常数.
对任意n(n∈N*)恒成立,其中k,b是常数.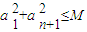 ,试求Sn的最大值.
,试求Sn的最大值.