题目内容
矩形ABCD中,AB=a,AD=b(a>b),沿对角线AC将△ADC折起,使AD与BC垂直,则异面直线AD与BC间的距离等于________.

分析:先证明BD是异面直线AD与BC的公垂线,然后在直角三角形ABD中求出BD的长即可.
解答:由于ABCD是矩形,则AB⊥BC,
因为AD⊥BC,故BC⊥平面ABD,即BC⊥BD;
又AD⊥DC,AD⊥BC,即AD⊥平面BCD,
即BD⊥AD,则BD是异面直线AD与BC的公垂线
在直角三角形ABD中,AB=a,BC=b(a>b),
故得BD=
 .
.故答案为:

点评:此题主要考查异面直线的角度及余弦值计算,同时考查了空间想象能力,属于基础题.

练习册系列答案
相关题目
 已知矩形ABCD中,AB=6,BC=6
已知矩形ABCD中,AB=6,BC=6 如图,在矩形ABCD中,
如图,在矩形ABCD中,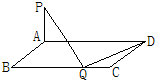 如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于
如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD,若在BC上只有一个点Q满足PQ⊥DQ,则a的值等于