题目内容
已知f(x)的定义域为{x∈R|x≠0},且f(x)是奇函数,当x>0时,f(x)=﹣x2+bx+c,若f(1)=f(3),f(2)=2
(1)求b,c的值;
(2)求f(x)在x<0时的表达式;
(3)若关于x的方程f(x)=ax,(a∈R)有解,求a的取值范围
(1)求b,c的值;
(2)求f(x)在x<0时的表达式;
(3)若关于x的方程f(x)=ax,(a∈R)有解,求a的取值范围
解:(1)由f(1)=f(3),f(2)=2
知,函数的顶点坐标为(2,2),
从而有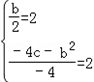 ,
,
∴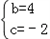 ;
;
(2)设x<0,则﹣x>0,
∴f(﹣x)=﹣x2﹣4x﹣2,
∵f(x)是奇函数,
∴﹣f(x)=﹣x2﹣4x﹣2,
∴f(x)=x2+4x+2(x<0);
(3)由题意,只需﹣x2+4x﹣2=ax在(0,+∞)上有解,
∴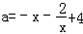
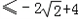 ,
,
即a的取值范围是 .
.
知,函数的顶点坐标为(2,2),
从而有
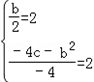 ,
,∴
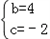 ;
;(2)设x<0,则﹣x>0,
∴f(﹣x)=﹣x2﹣4x﹣2,
∵f(x)是奇函数,
∴﹣f(x)=﹣x2﹣4x﹣2,
∴f(x)=x2+4x+2(x<0);
(3)由题意,只需﹣x2+4x﹣2=ax在(0,+∞)上有解,
∴
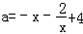
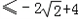 ,
,即a的取值范围是
 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知f(x)的定义域为[-1,2),则f(|x|)的定义域为( )
| A、[-1,2) | B、[-1,1] | C、(-2,2) | D、[-2,2) |