题目内容
(本题14分)已知函数![]()
⑴当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
⑵若关于![]() 的方程
的方程![]() 有两个大于0的实根,求
有两个大于0的实根,求![]() 的取值范围;
的取值范围;
⑶当![]() 时,求函数
时,求函数![]() 的最小值。
的最小值。
(本题14分)
解:⑴设![]() ,则
,则![]() -------1
-------1
当![]() 时,
时,![]() ,对称轴为
,对称轴为![]() ,开口向上 -------2
,开口向上 -------2
![]() 单调递增
单调递增 ![]()
![]() 函数
函数![]() 的值域为
的值域为![]() -------4
-------4
⑵由![]()
方程![]() 有两个大于0的实根等价于方程
有两个大于0的实根等价于方程![]() 有两个大于1的实根,------5
有两个大于1的实根,------5
则需 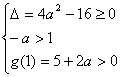 解得
解得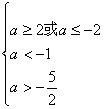
![]() -----9
-----9
⑶由![]() 得
得![]() ------10
------10
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,![]()
当![]() ,即
,即![]() 时,
时,![]()
当![]() 即
即![]() 时,
时,![]() 在
在![]() 单调递增,
单调递增,![]()
(说明单调性1分) ------14

练习册系列答案
相关题目
 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。