题目内容
 已知直线l:ax-y+
已知直线l:ax-y+| 2 |
(Ⅰ)求证:直线l与圆O相交;
(Ⅱ)判断直线l被圆O截得的弦何时最短?并求出最短弦的长度;
(Ⅲ)如图,已知AC、BD为圆O的两条相互垂直的弦,垂足为M(1,
| 2 |
分析:(Ⅰ)判断直线恒过定点,证明点在圆的内部,即可得到结论;
(Ⅱ)由(Ⅰ)可知,直线l过定点M(1,
),当l⊥OM时,弦长最短;
(Ⅲ)设圆心O到AC、BD的距离为d1、d2,垂足分别为E、F,则四边形OEMF为矩形,则有d12+d22=3,表示出AC,BD,可得四边形ABCD的面积,利用基本不等式,即可求得最大值.
(Ⅱ)由(Ⅰ)可知,直线l过定点M(1,
| 2 |
(Ⅲ)设圆心O到AC、BD的距离为d1、d2,垂足分别为E、F,则四边形OEMF为矩形,则有d12+d22=3,表示出AC,BD,可得四边形ABCD的面积,利用基本不等式,即可求得最大值.
解答:(Ⅰ)证明:直线l:y-
=a(x-1),所以直线l过定点(1,
),
∵12+(
)2<4,∴(1,
)在圆C内部,
∴直线l与圆C相交.…3分
(Ⅱ)解:由(Ⅰ)可知,直线l过定点M(1,
),当l⊥OM时,弦长最短.…4分
∴kl=-
=-
,∴a=-
此时,l的方程为x+
y-3=0,圆心到直线的距离d=
=
所以最短弦长:2
=2
=2…7分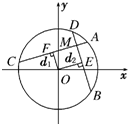
(Ⅲ)解:设圆心O到AC、BD的距离为d1、d2,垂足分别为E、F,则四边形OEMF为矩形,则有d12+d22=3
由平面几何知识知:|AC|=2
,|BD|=2
∴S四边形ABCD=
|AC|•|BD|=2
≤(4-d12)+(4-d22)
=8-(d12+d22)=5(当且仅当d1=d2取等号)
∴四边形ABCD的面积的最大值为5.…12分.
| 2 |
| 2 |
∵12+(
| 2 |
| 2 |
∴直线l与圆C相交.…3分
(Ⅱ)解:由(Ⅰ)可知,直线l过定点M(1,
| 2 |
∴kl=-
| 1 |
| kOM |
| ||
| 2 |
| ||
| 2 |
此时,l的方程为x+
| 2 |
| 3 | ||
|
| 3 |
所以最短弦长:2
| r2-d2 |
| 4-3 |

(Ⅲ)解:设圆心O到AC、BD的距离为d1、d2,垂足分别为E、F,则四边形OEMF为矩形,则有d12+d22=3
由平面几何知识知:|AC|=2
| 4-d12 |
| 4-d22 |
∴S四边形ABCD=
| 1 |
| 2 |
| 4-d12 |
| 4-d22 |
=8-(d12+d22)=5(当且仅当d1=d2取等号)
∴四边形ABCD的面积的最大值为5.…12分.
点评:本题考查直线与圆的位置关系,考查圆中弦长的计算,考查基本不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目