Question

已知O是△ABC的外心，AB=2，AC=3，x+2y=1，若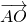=x•+y•，（xy≠0），则cos∠BAC=________．

Answer 1

分析：设出A，C，∠BAC=α，B（2cosα，2sinα），O是△ABC的外心，所以O的横坐标是，利用x+2y=1，若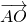=x•+y•，求出cosα，即可．
解答：设A（0，0），C（3，0），∠BAC=α
B（2cosα，2sinα）
O是△ABC的外心，所以O的横坐标是，
因为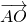=x•+y•，
所以：=x2cosα+3y
因为x+2y=1，所以x+3y=
x2cosα+3y=x+3y
2cosα=，即：cos∠BAC=
故答案为：
点评：本题考查三角形五心，向量的共线定理，考查计算能力，是基础题．