题目内容
设f(x)在R上是偶函数,在区间(-∞,0)上递增,且有f(2a2+a+1)<f(3a2-2a+1),求a的取值范围.
解析:要求a的取值范围,就要布列关于a的不等式(组),因而利用函数的单调性、奇偶性化“抽象的不等式”为“具体的代数式”是关键.
答案:由f(x)在R上是偶函数,在区间(-∞,0)上递增知f(x)在(0,+∞)上递减.
∵2a2+a+1=2(a+![]() )2+
)2+![]() >0,3a2-2a+1=3(a-
>0,3a2-2a+1=3(a-![]() )2+
)2+![]() >0,
>0,
且f(2a2-2a+1)<f(3a2-2a+1),
∴2a2+a+1>3a2-2a+1,
即a2-3a<0.
解之得0<a<3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
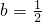 ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由. ,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.
,且k>0,问函数f(x)的图象是不是轴对称图形?如果是,求出函数f(x)图象的对称轴;如果不是,请说明理由.