题目内容
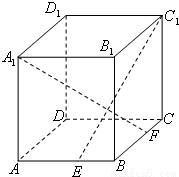
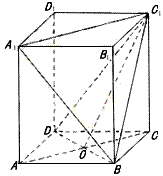
如图,ABCD-A1B1C1D1是正四棱柱,
(Ⅰ)求证:BD⊥平面ACC1A1;
(Ⅱ)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小。
(Ⅰ)求证:BD⊥平面ACC1A1;
(Ⅱ)若二面角C1-BD-C的大小为60°,求异面直线BC1与AC所成角的大小。
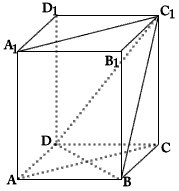
| (Ⅰ)证明:∵ABCD-A1B1C1D1是正四棱柱, ∴CC1⊥平面ABCD,∴BD⊥CC1, ∵ABCD是正方形, ∴BD⊥AC, 又∵AC,CC1  平面ACC1A1,且AC∩CC1=C, 平面ACC1A1,且AC∩CC1=C,∴BD⊥平面ACC1A1。 |
|
| (Ⅱ)解:设BD与AC相交于O,连接C1O, ∵CC1⊥平面ABCD,BD⊥AC, ∴BD⊥C1O, ∴∠C1OC是二面角C1-BD-C的平面角, ∴∠C1OC=60°,连接A1B, ∵A1C1∥AC, ∴∠A1C1B是BC1与AC所成角, 设BC=a,则CO= 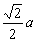 ,CC1=CO·tan60°= ,CC1=CO·tan60°=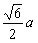 , ,A1B=BC1= 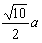 ,A1C1= ,A1C1=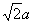 , ,在△A1BC1中, 由余弦定理得cosA1C1B= 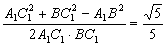 , ,∴∠A1C1B=arccos 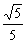 , ,∴异面直线BC1与AC所成角的大小为arccos 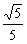 。 。 |
 |

练习册系列答案
相关题目
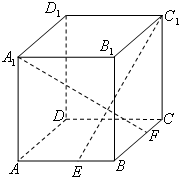 如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF.
如图,ABCD-A1B1C1D1是棱长为6的正方体,E、F分别是棱AB、BC上的动点,且AE=BF. 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的是 如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,下面结论中正确的结论是