题目内容
(本题满分13分)
如图,在三棱 柱
柱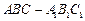 中,已知
中,已知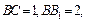
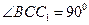 ,
,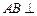 侧面
侧面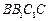
(1)求直线C1B与底面ABC所成角的正弦值;
(2)在棱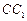 (不包含端点
(不包含端点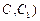 上确定一点
上确定一点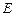 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(3)在(2)的条件下,若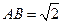 ,求二面角
,求二面角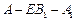 的大小.
的大小.
如图,在三棱
 柱
柱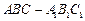 中,已知
中,已知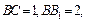
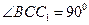 ,
,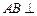 侧面
侧面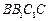
(1)求直线C1B与底面ABC所成角的正弦值;

(2)在棱
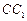 (不包含端点
(不包含端点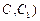 上确定一点
上确定一点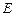 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).(3)在(2)的条件下,若
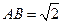 ,求二面角
,求二面角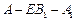 的大小.
的大小.解:如图,以B为原点建立空间直角坐标系 ,则
,则 ,
, ,
,

(1)直三棱柱 中,
中,
平面 的法向量
的法向量 ,又
,又 ,
,
设 ,则
,则
 4分
4分
(2)设 ,则
,则 ,
,
 ,∴
,∴
 ,
,
即

 8分
8分
(3)∵AB= ,从而
,从而 ,则
,则 ,
,
设平面 的法向量
的法向量 

则

 ,取
,取
 ,
,
∵ ,
, ∴
∴ ,又
,又
 ,
,
∴平面 的法向量
的法向量 ,∴
,∴
 ,
,
∴二面角 为45°.
为45°. 13分
13分
 ,则
,则 ,
, ,
,

(1)直三棱柱
 中,
中,平面
 的法向量
的法向量 ,又
,又 ,
,设
 ,则
,则
 4分
4分 (2)设
 ,则
,则 ,
,
 ,∴
,∴
 ,
,即


 8分
8分
(3)∵AB=
 ,从而
,从而 ,则
,则 ,
,设平面
 的法向量
的法向量 

则


 ,取
,取
 ,
,∵
 ,
, ∴
∴ ,又
,又
 ,
,∴平面
 的法向量
的法向量 ,∴
,∴
 ,
,∴二面角
 为45°.
为45°. 13分
13分 略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
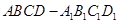 的侧棱长为2,
的侧棱长为2,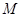 为
为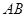 的中点,则异面直线
的中点,则异面直线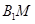 与
与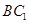 所成角的大小为( )
所成角的大小为( )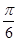
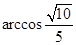
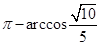
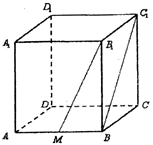
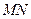 和
和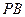 是两条面对角线,请在图(2)的正方体中将
是两条面对角线,请在图(2)的正方体中将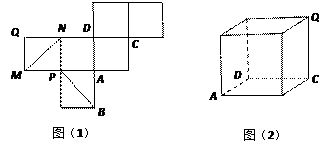
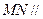 平面
平面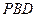 ;
;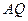 ⊥平面
⊥平面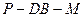 的大小.
的大小.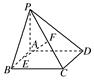
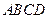 的边长为
的边长为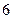 ,
,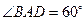 ,
,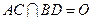 .将菱形
.将菱形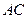 折起,使
折起,使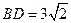 ,得到三棱锥
,得到三棱锥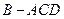 .
.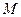 是棱
是棱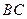 的中点,求证:
的中点,求证: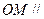 平面
平面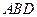 ;
; 的余弦值;
的余弦值;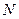 是线段
是线段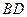 上一个动点,试确定
上一个动点,试确定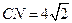 ,并证明你的结论
,并证明你的结论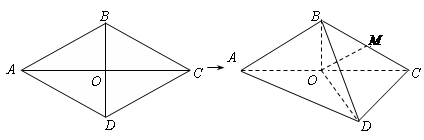
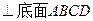
 明:AB
明:AB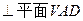 ;
; 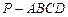 的底面
的底面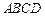 为菱形,
为菱形,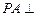 平面
平面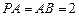 ,
,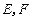 分别为
分别为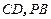 的中点,
的中点,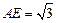 .
.
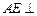 平面
平面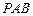 .
.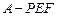 的体积.
的体积.
 (本小题满分12分)
(本小题满分12分)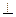 平面ABCD,PD=AD=2。
平面ABCD,PD=AD=2。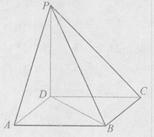
 平面ADE?并说明理由。
平面ADE?并说明理由。