题目内容
12.设函数f(x)=-lnx+x2.(1)判断f(x)的单调性;
(2)求f(x)在区间[$\frac{1}{4}$,$\frac{3}{4}$]上的最大值和最小值.
分析 (1)先求函数f(x)=-lnx+x2的定义域,再求导f′(x)=-$\frac{1}{x}$+2x=$\frac{(\sqrt{2}x+1)(\sqrt{2}x-1)}{x}$;从而由导数的正负确定函数的单调性;
(2)由(1)知f(x)在区间[$\frac{1}{4}$,$\frac{\sqrt{2}}{2}$]上是减函数,在[$\frac{\sqrt{2}}{2}$,$\frac{3}{4}$]上是增函数,从而求闭区间上的最值.
解答 解:(1)f(x)=-lnx+x2的定义域为(0,+∞),
f′(x)=-$\frac{1}{x}$+2x=$\frac{(\sqrt{2}x+1)(\sqrt{2}x-1)}{x}$;
∴当x∈(0,$\frac{\sqrt{2}}{2}$)时,f′(x)<0,
当x∈($\frac{\sqrt{2}}{2}$,+∞)时,f′(x)>0,
∴f(x)的单调减区间为(0,$\frac{\sqrt{2}}{2}$),单调增区间为($\frac{\sqrt{2}}{2}$,+∞);
(2)由(1)知,
f(x)在区间[$\frac{1}{4}$,$\frac{\sqrt{2}}{2}$]上是减函数,在[$\frac{\sqrt{2}}{2}$,$\frac{3}{4}$]上是增函数,
fmax(x)=f($\frac{\sqrt{2}}{2}$)=$\frac{1}{2}$+$\frac{1}{2}$ln2,
f($\frac{1}{4}$)=$\frac{1}{16}$+ln4,f($\frac{3}{4}$)=$\frac{9}{16}$+ln4-ln3=$\frac{1}{16}$+ln4+$\frac{1}{2}$-ln3<$\frac{1}{16}$+ln4;
故fmin(x)=f($\frac{3}{4}$)=$\frac{9}{16}$+ln4-ln3.
点评 本题考查了导数的综合应用及闭区间上最值的求法,属于中档题.

| A. | 偶函数,且单调递增 | B. | 偶函数,且单调递减 | ||
| C. | 奇函数,且单调递增 | D. | 奇函数,且单调递减 |
| A. | $\frac{π}{3}$ | B. | $\frac{5π}{12}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
| A. | 在△ABC中,角A,B所对边分别为a,b则sinA>sinB成立的充要条件是a>b | |||||||||
| B. | 若命题p:?x∈(0,+∞),sinx-x<0,命题q:?x0∈(0,+∞),e${\;}^{{x}_{0}}$<0,则p∧¬q为真命题 | |||||||||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则存在唯一的实数λ,使$\overrightarrow{a}$=λ$\overrightarrow{b}$ | |||||||||
| D. | 在一个2×2列联表中,由计算得k2=6.721,则有99%的把握确认这两个变量间有关系;可以参考独立性检验临界表
|
 某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )
某中学为了解高三学生数学课程的学习情况,从全部2000名学生的数学考试成绩中随机抽取部分学生的考试成绩进行统计分析,得到如下的样本的频率分布直方图,已知成绩在[80,90)的学生共有40人,则样本中成绩在[60,80)内的人数为( )| A. | 102 | B. | 104 | C. | 112 | D. | 114 |
| A. | (-1,0) | B. | (0,1) | C. | (1,2) | D. | (2,3) |
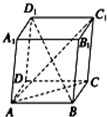 如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )
如图,平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长都相等,且它们彼此的夹角都是60°;记AC1=λAB,则λ的值为( )| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |