题目内容
若点 在椭圆
在椭圆 上,
上, 、
、 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且 ,则
,则 的面积是 ( )
的面积是 ( )
| A.2 | B.1 | C. | D. |
B
解析考点:椭圆的简单性质.
分析:由椭圆的定义可得 m+n="2a=2"  ①,Rt△F1PF2中,由勾股定理可得m
①,Rt△F1PF2中,由勾股定理可得m +n
+n =4②,由①②可得m?n的值,利用△F1PF2的面积是
=4②,由①②可得m?n的值,利用△F1PF2的面积是  m?n求得结果.
m?n求得结果.
解答:解:由椭圆的方程可得 a= ,b=1,c=1,令|F
,b=1,c=1,令|F P|=m、|PF
P|=m、|PF |=n,
|=n,
由椭圆的定义可得 m+n=2a=2 ①,Rt△F
①,Rt△F PF
PF 中,
中,
由勾股定理可得(2c) =m
=m +n
+n ,m
,m +n
+n =4②,由①②可得m?n=2,
=4②,由①②可得m?n=2,
∴△F PF
PF 的面积是
的面积是 m?n=1,
m?n=1,
故选B.

练习册系列答案
相关题目
平面直角坐标系中,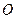 为坐标原点,已知两点
为坐标原点,已知两点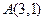 ,
,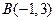 ,若点
,若点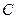 满足
满足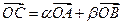 ,其中
,其中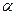 、
、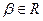 且
且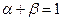 ,则点
,则点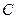 的轨迹方程为 ( )
的轨迹方程为 ( )
A.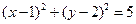 | B.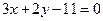 |
C.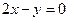 | D.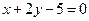 |
若点O和点F分别为椭圆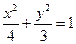 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则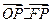 的最大值为
的最大值为
| A.8 | B.6 | C.3 | D.2 |
若椭圆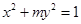 的离心率为
的离心率为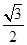 ,则它的长半轴长为( )
,则它的长半轴长为( )
| A.1 | B.2 | C.1或2 | D.与m有关 |
 ,则方程
,则方程 表示的曲线只可能是
表示的曲线只可能是
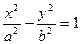 的一条渐近线与抛物线y=x
的一条渐近线与抛物线y=x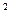 +1 只有一个公共点,则双曲线的离心率为( )
+1 只有一个公共点,则双曲线的离心率为( )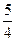
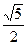

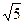




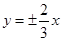
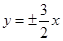
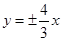
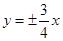
 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2是锐角三角形,则该双曲线离心率的取值范围( ) (B)
(B) (C)
(C) (D)
(D) 