Question

一块直径为30 cm的圆形铁板，已经截去直径分别为20 cm，10 cm的圆形铁板各一块，现要求在所剩余的铁板中，再截出同样大小的铁板两块，问：这两块铁板的半径最大有多少厘米？

Answer 1

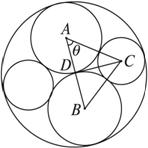
思路分析：如图，圆A与圆B为已截去的圆，则需要再截去的圆与圆A、圆B均相切.图中的圆C是其中之一，所以可通过解三角形ABC来解决问题，在应用两圆的位置关系解题时，要注意两圆外切时，圆心距是两圆半径的和，而两圆内切时，圆心距是两圆半径差的绝对值.

解：设大圆圆心为D，圆A与圆B外切且圆A、圆B都与圆D内切，D在线段AB上，根据题意,所求的圆C与圆A、圆B都外切，且与圆D内切.连结AC、AB、BC.

设所求最大圆的半径为x，∠BAC=θ，则在△ABC中，AB=15，AC=10+x，BC=5+x，根据余弦定理有

cosθ=.

又在△ACD中,AD=5，AC=10+x，CD=15－x.

由余弦定理,得cosθ=.

∴7x²+40x－300=0?x₁=,x₂=－10(舍去),

即在剩余的铁板中还可以截去半径最大为cm的同样大小的圆形铁板两块.