题目内容
函数f(x)=lg(|x|-1)
A、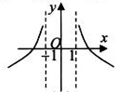 | B、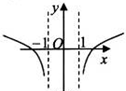 | C、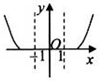 | D、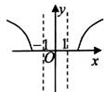 |
分析:根据对数函数的图和性质,进行判断即可.
解答:解:由|x|-1>0,解得x>1或x<-1,
∵f(x)=lg(|x|-1),
∴当x>1时,f(x)=lg(x-1),此时函数f(x)单调递增,
且函数f(-x)=f(x)为偶函数,
∴对应的图象为B,
故选:B.
∵f(x)=lg(|x|-1),
∴当x>1时,f(x)=lg(x-1),此时函数f(x)单调递增,
且函数f(-x)=f(x)为偶函数,
∴对应的图象为B,
故选:B.
点评:本题主要考查函数图象的识别和判断,利用对数函数的性质是解决本题的关键.

练习册系列答案
相关题目