题目内容
(不等式选讲选做题)
(1)已知实数a、b、x、y满足a2+b2=1,x2+y2=3,求ax+by的最大值;
(2)若x<1,求2-x+
的最小值,并求此时x的值.
(1)已知实数a、b、x、y满足a2+b2=1,x2+y2=3,求ax+by的最大值;
(2)若x<1,求2-x+
| 4 | (x-1)2 |
分析:(1)先根据柯西不等式可知(a2+b2)(x2+y2)≥(ax+by)2,进而的求得(ax+by)2的最大值,进而求得ax+by的最大值.
(2)先将2-x+
凑成=1+
+
+
,然后利用基本不等式求出函数的最值,检验等号何时成立.
(2)先将2-x+
| 4 |
| (x-1)2 |
| 1-x |
| 2 |
| 1-x |
| 2 |
| 4 |
| (x-1)2 |
解答:解:(1)因为a2+b2=1,x2+y2=3,
由柯西不等式(a2+b2)(x2+y2)≥(ax+by)2,得
3≥(ax+by)2,
所以ax+by的最大值为
.
(2)2-x+
=1+
+
+
≥1+3
=4
当且仅当
=
=
即x=-1时取等号.
最小值为4,此时x的值为-1.
由柯西不等式(a2+b2)(x2+y2)≥(ax+by)2,得
3≥(ax+by)2,
所以ax+by的最大值为
| 3 |
(2)2-x+
| 4 |
| (x-1)2 |
=1+
| 1-x |
| 2 |
| 1-x |
| 2 |
| 4 |
| (x-1)2 |
≥1+3
| 3 |
| ||||||
=4
当且仅当
| 1-x |
| 2 |
| 1-x |
| 2 |
| 4 |
| (x-1)2 |
最小值为4,此时x的值为-1.
点评:本题主要考查了基本不等式在最值问题中的应用.解题的关键是利用了柯西不等式,达到解决问题的目的.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
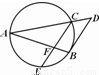
 ,则线段CD的长为 .
,则线段CD的长为 .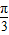 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .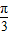 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .