题目内容
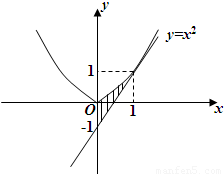
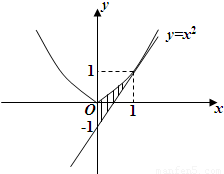
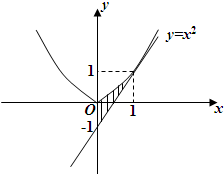抛物线y=x2在A（1，1）处的切线与y轴及该抛物线所围成的图形面积为（ ）分析：先求切线方程，再用定积分求图形面积，求出被积函数的原函数即可．
解答：
解：先求导函数，可得y′=2x，
∴抛物线y=x2在A（1，1）处的切线的斜率为2
∴切线为y=2x-1，由定积分的几何意义得，所求图形的面积为
A=
[x2-(2x-1)]dx=(
x3-x2+x)
故选A．
解：先求导函数，可得y′=2x，∴抛物线y=x2在A（1，1）处的切线的斜率为2
∴切线为y=2x-1，由定积分的几何意义得，所求图形的面积为
A=
| ∫ | 1 0 |
| 1 |
| 3 |
|
故选A．
点评：本题考查了根据导数几何意义求切线方程，再根据定积分的几何意义求平面图形的面积，是一道小综合题．
练习册系列答案
阅读快车系列答案
相关题目
点”，那么下列结论中正确的是（ ）
