题目内容
定义在R上的函数f(x)满足:对任意的x1,x2∈R(x1≠x2),有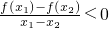 恒成立,若a=f(log279),b=f((
恒成立,若a=f(log279),b=f(( )
) ),c=f(-ln
),c=f(-ln ),则
),则
- A.b<a<c
- B.a<b<c
- C.c<a<b
- D.c<b<a
A
分析:函数是R上的减函数,化简a=f( ),b=f(
),b=f( ),c=f(-
),c=f(- ),由此可得a、b、c的大小关系.
),由此可得a、b、c的大小关系.
解答:∵定义在R上的函数f(x)满足:对任意的x1,x2∈R(x1≠x2),有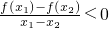 恒成立,
恒成立,
∴函数是R上的减函数.
由于a=f(log279)=f( )=f(
)=f( ),b=f((
),b=f(( )
) )=f(
)=f( ),c=f(-ln
),c=f(-ln )=f(-ln
)=f(-ln )=f(-
)=f(- ),而且
),而且 >
> >-
>- ,
,
∴b<a<c,
故选A.
点评:本题主要考查指数型复合函数、对数型的性质以及函数的单调性的应用,判断函数是R上的减函数,是解题的关键,属于中档题.
分析:函数是R上的减函数,化简a=f(
 ),b=f(
),b=f( ),c=f(-
),c=f(- ),由此可得a、b、c的大小关系.
),由此可得a、b、c的大小关系.解答:∵定义在R上的函数f(x)满足:对任意的x1,x2∈R(x1≠x2),有
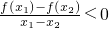 恒成立,
恒成立,∴函数是R上的减函数.
由于a=f(log279)=f(
 )=f(
)=f( ),b=f((
),b=f(( )
) )=f(
)=f( ),c=f(-ln
),c=f(-ln )=f(-ln
)=f(-ln )=f(-
)=f(- ),而且
),而且 >
> >-
>- ,
,∴b<a<c,
故选A.
点评:本题主要考查指数型复合函数、对数型的性质以及函数的单调性的应用,判断函数是R上的减函数,是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目