题目内容
在平面四边形ABCD中，向量
=
=(4，1)，
=
=(3，-1)，
=
=(-1，-2)．
（Ⅰ）若向量(
+2
)与向量(
-k
)垂直，求实数k的值；
（Ⅱ）若
=m
+n
，求实数m，n．
| a |
| AB |
| b |
| BC |
| c |
| CD |
（Ⅰ）若向量(
| a |
| b |
| b |
| c |
（Ⅱ）若
| DB |
| DA |
| DC |
分析：（I）根据向量(
+2
)与向量(
-k
)垂直可知两向量的数量积为0，建立方程，解之即可求出k的值；
（II）根据
=
+
求出
的坐标，然后根据
=
+
+
求出
的坐标，最后根据
=m
+n
，建立关于m，n的方程组，解之即可．
| a |
| b |
| b |
| c |
（II）根据
| BD |
| BC |
| CD |
| BD |
| AD |
| AB |
| BC |
| CD |
| AD |
| DB |
| DA |
| DC |
解答：解：（Ⅰ）∵向量(
+2
)与向量(
-k
)垂直
∴(
+2
)•(
-k
)=0…（2分）
∴（10，-1）•（3+k，-1+2k）=0
∴30+10k+1-2k=0∴k=-
…（5分）
（Ⅱ）
=
+
=(2，-3)，∴
=(-2，3)…（7分）
=
+
+
=(6，-2)∴
=(-6，2)，
=(1，2)…（9分）
∵
=m
+n
，
∴（-2，3）=m（-6，2）+n（1，2）
∴
∴m=
，n=1…（12分）
| a |
| b |
| b |
| c |
∴(
| a |
| b |
| b |
| c |
∴（10，-1）•（3+k，-1+2k）=0
∴30+10k+1-2k=0∴k=-
| 31 |
| 8 |
（Ⅱ）
| BD |
| BC |
| CD |
| DB |
| AD |
| AB |
| BC |
| CD |
| DA |
| DC |
∵
| DB |
| DA |
| DC |
∴（-2，3）=m（-6，2）+n（1，2）
∴
|
∴m=
| 1 |
| 2 |
点评：本题主要考查了平面向量数量积的运算，以及向量的坐标运算，同时考查了运算求解的能力，属于中档题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
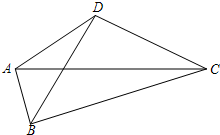
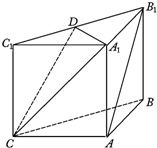如图，在三棱柱ABC-A1B1C1中，侧面ABB1A1，ACC1A1均为正方形，∠BAC=90°，点D是棱B1C1的中点．
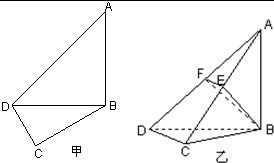在平面四边形ABCD中，已知∠A=45°，∠C=90°，∠ADC=105°，AB=BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC（如图乙），设点E、F分别为棱AC、AD的中点．
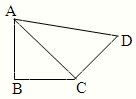如图，在平面四边形ABCD中，AB=BC=CD=a，∠ABC=90°，∠BCD=135°，沿对角线AC将此四边形折成直二面角．
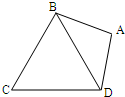（2007•武汉模拟）如图，在平面四边形ABCD中，AB=AD=1，∠BAD=θ，而△BCD是正三角形，