题目内容
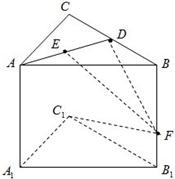 已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,BF=BC=2,FB1=1,D为BC中点,E为线段AD上不同于A、D的任意一点,
已知直三棱柱ABC-A1B1C1,AB=AC,F为BB1上一点,BF=BC=2,FB1=1,D为BC中点,E为线段AD上不同于A、D的任意一点,(1)证明:EF⊥FC1;
(2)若AB=
| 2 |
| ||
| 6 |
分析:(1)由题意先证明AD⊥面B1BCC1,得AD⊥C1F;再利用Rt△DBF 1≌Rt△FB1C证明C1F⊥FD,可得C1F⊥面DEF;即可得证;
(2)先假设存在,建立坐标系求出平面FA1C1的法向量,利用向量数量积列出EF与平面FA1C1所成角的余弦值求解即可.
(2)先假设存在,建立坐标系求出平面FA1C1的法向量,利用向量数量积列出EF与平面FA1C1所成角的余弦值求解即可.
解答:解:(1)∵AB=AC,D为BC中点,∴AD⊥BC
∵三棱柱ABC-A1B1C1为直三棱锥,∴B1B⊥面ABC
∴BB1⊥AD,BC∩BB1=B,
∴AD⊥面B1BCC1,C1F?面B1BCC1
∴AD⊥C1F;∵BC=BF=2,∴DB=1,又∵FB1=1
∴Rt△DBF 1≌Rt△FB1C,∴∠DBF+∠C1FB1=
,
∴∠DFC1=
∴C1F⊥FD,
∴C1F⊥面DEF,∴C1F⊥EF
(2)以A1为坐标原点,A1B1、A1C1、A1A所在直线为x,y,z轴建立如图所示空间直角坐标系,
∴
=(0,
,0),
=(
,0,1),
设面A1FC1的法向量为
=(x,y,z),则有
•
=0,
•
=0可得
=(1,0,-
),D(
,
,3)
设E(
t,
t,3)(0<t<1),
∴
=(
t-
,
t,2),由已知
=
.
整理得2t2+t-3=0,解之得t=-
或t=1
∴不存在合适的点E.
∵三棱柱ABC-A1B1C1为直三棱锥,∴B1B⊥面ABC
∴BB1⊥AD,BC∩BB1=B,
∴AD⊥面B1BCC1,C1F?面B1BCC1
∴AD⊥C1F;∵BC=BF=2,∴DB=1,又∵FB1=1
∴Rt△DBF 1≌Rt△FB1C,∴∠DBF+∠C1FB1=
| π |
| 2 |
∴∠DFC1=
| π |
| 2 |
∴C1F⊥面DEF,∴C1F⊥EF
(2)以A1为坐标原点,A1B1、A1C1、A1A所在直线为x,y,z轴建立如图所示空间直角坐标系,
∴
| A1C1 |
| 2 |
| A1F |
| 2 |
设面A1FC1的法向量为
| n |
| n |
| A1C1 |
| n |
| A1F |
| n |
| 2 |
| ||
| 2 |
| ||
| 2 |
设E(
| ||
| 2 |
| ||
| 2 |
∴
| FE |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 6 |
|
| ||||
|
|
整理得2t2+t-3=0,解之得t=-
| 3 |
| 2 |
∴不存在合适的点E.
点评:本题先根据线面垂直的定义和判定定理证明线线垂直;对于线面角问题用向量求解要简单,此题需要
根据题意列出满足题意的式子求解,判断是否存在合适的点.
根据题意列出满足题意的式子求解,判断是否存在合适的点.

练习册系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.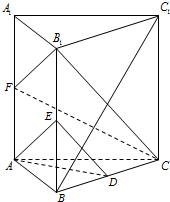 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.