题目内容
【题目】在数列![]() 中,
中,![]() ,且对任意
,且对任意![]() ,
,![]() 成等差数列,其公差为
成等差数列,其公差为![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,证明
,证明![]() 成等比数列(
成等比数列(![]() );
);
(3)若对任意![]() ,
,![]() 成等比数列,其公比为
成等比数列,其公比为![]() ,设
,设![]() ,证明数列
,证明数列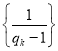 是等差数列.
是等差数列.
【答案】(1)![]() ,
,![]() .(2)见证明;(3)见证明;
.(2)见证明;(3)见证明;
【解析】
(1)由![]() 成等差数列且公差为2可计算
成等差数列且公差为2可计算![]() 的值.
的值.
(2)由![]() 可得
可得![]() ,再根据
,再根据![]() 得到
得到![]() ,从而可证
,从而可证![]() 成等比数列.
成等比数列.
(3)利用![]() 成等比数列且公比为
成等比数列且公比为![]() 可得
可得![]() ,对该递推关系变形后可得
,对该递推关系变形后可得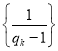 为等差数列.
为等差数列.
(1)因为对任意![]() ,
,![]() 成等差数列,
成等差数列,
所以当![]() 时,
时,![]() 成等差数列且公差为2,
成等差数列且公差为2,
故![]() ,故
,故![]() .
.
(2)证明:由题设,可得![]() ,
,![]() .所以
.所以![]()
![]() ,
,
由![]() 得,
得,![]() ,
,
从而![]() ,所以
,所以![]() .
.
于是![]() ,
,
所以当![]() 时,对任意的
时,对任意的![]() ,
,![]() 成等比数列.
成等比数列.
(3)由![]() 成等差数列,及
成等差数列,及![]() 成等比数列,
成等比数列,
可得![]() ,所以
,所以![]() ,
,
当![]() 时,可知
时,可知![]() ,
,![]() ,
,
从而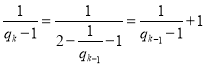 ,即
,即![]() ,
,
所以数列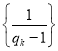 是公差为1的等差数列.
是公差为1的等差数列.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
【题目】2019年4月,甲乙两校的学生参加了某考试机构举行的大联考,现对这两校参加考试的学生的数学成绩进行统计分析,数据统计显示,考生的数学成绩![]() 服从正态分布
服从正态分布![]() ,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
,从甲乙两校100分及以上的试卷中用系统抽样的方法各抽取了20份试卷,并将这40份试卷的得分制作成如图所示的茎叶图:
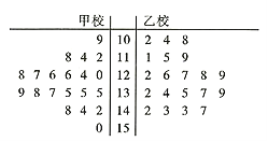
(1)试通过茎叶图比较这40份试卷的两校学生数学成绩的中位数;
(2)若把数学成绩不低于135分的记作数学成绩优秀,根据茎叶图中的数据,判断是否有![]() 的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
的把握认为数学成绩在100分及以上的学生中数学成绩是否优秀与所在学校有关?
(3)从所有参加此次联考的学生中(人数很多)任意抽取3人,记数学成绩在134分以上的人数为![]() ,求
,求![]() 的数学期望.
的数学期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]()
![]() ,
,![]() .
.
参考公式与临界值表:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |