题目内容
如图,椭圆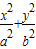 =1(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且
=1(a>b>0)的左、右焦点分别为F1、F2,M、N是椭圆右准线上的两个动点,且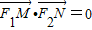 .
.(1)设C是以MN为直径的圆,试判断原点O与圆C的位置关系;
(2)设椭圆的离心率为
 ,MN的最小值为
,MN的最小值为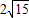 ,求椭圆方程.
,求椭圆方程.
【答案】分析:(1)C是以MN为直径的圆,求出M,N的坐标,利用 ,判断
,判断 ,求得原点O在圆C的内部;
,求得原点O在圆C的内部;
(2)设椭圆的离心率为 ,推出a=2c,利用基本不等式,通过MN的最小值为
,推出a=2c,利用基本不等式,通过MN的最小值为 求出c,a,b,从而求出椭圆方程.
求出c,a,b,从而求出椭圆方程.
解答:解:(1)设椭圆 的焦距为2c(c>0),
的焦距为2c(c>0),
则其右准线方程为x= ,且F1(-c,0),F2(c,0).
,且F1(-c,0),F2(c,0).
设 ,
,
则
 .
.
因此
即 .
.
于是 ,故∠MON为锐角.
,故∠MON为锐角.
所以原点O在圆C外.
(2)因为椭圆的离心率为 ,所以a=2c,
,所以a=2c,
于是M(4c,y1)N(4c,y2),且
MN2=(y1-y2)2=y12+y22-2y1y2=|y1|2+|y2|2+2|y1y2|≥4|y1y2|=60c2.
当且仅当y1=-y2= 或y2=-y1=
或y2=-y1= 时取“=”号,
时取“=”号,
所以(MN)min=2 c=2
c=2 ,于是c=1,从而a=2,b=
,于是c=1,从而a=2,b= ,
,
故所求的椭圆方程是 .
.
点评:本题考查点与圆的位置关系,椭圆的标准方程,考查分析问题解决问题的能力,考查计算能力,是中档题.
 ,判断
,判断 ,求得原点O在圆C的内部;
,求得原点O在圆C的内部;(2)设椭圆的离心率为
 ,推出a=2c,利用基本不等式,通过MN的最小值为
,推出a=2c,利用基本不等式,通过MN的最小值为 求出c,a,b,从而求出椭圆方程.
求出c,a,b,从而求出椭圆方程.解答:解:(1)设椭圆
 的焦距为2c(c>0),
的焦距为2c(c>0),则其右准线方程为x=
 ,且F1(-c,0),F2(c,0).
,且F1(-c,0),F2(c,0).设
 ,
,则

 .
.因此

即
 .
.于是
 ,故∠MON为锐角.
,故∠MON为锐角.所以原点O在圆C外.
(2)因为椭圆的离心率为
 ,所以a=2c,
,所以a=2c,于是M(4c,y1)N(4c,y2),且

MN2=(y1-y2)2=y12+y22-2y1y2=|y1|2+|y2|2+2|y1y2|≥4|y1y2|=60c2.
当且仅当y1=-y2=
 或y2=-y1=
或y2=-y1= 时取“=”号,
时取“=”号,所以(MN)min=2
 c=2
c=2 ,于是c=1,从而a=2,b=
,于是c=1,从而a=2,b= ,
,故所求的椭圆方程是
 .
.点评:本题考查点与圆的位置关系,椭圆的标准方程,考查分析问题解决问题的能力,考查计算能力,是中档题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 =1(a>b>0)与过A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过A(2,0),B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
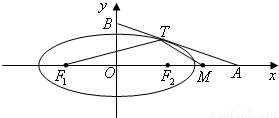
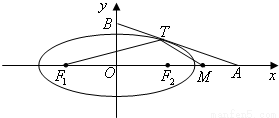
 如图,椭圆
如图,椭圆 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e= .
. 如图,椭圆
如图,椭圆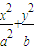 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=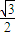 .
.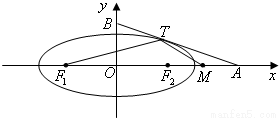 如图,椭圆
如图,椭圆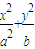 =1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=
=1(a>b>0)与过点A(2,0)B(0,1)的直线有且只有一个公共点T,且椭圆的离心率e=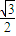 .
. =1(a>b>0)与一等轴双曲线相交,M是其中一个交点,并且双曲线的顶点是该椭圆的焦点F1,F2,双曲线的焦点是椭圆的顶点A1,A2,△MF1F2的周长为4(
=1(a>b>0)与一等轴双曲线相交,M是其中一个交点,并且双曲线的顶点是该椭圆的焦点F1,F2,双曲线的焦点是椭圆的顶点A1,A2,△MF1F2的周长为4( +1).设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1).设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.