题目内容
如果存在实数x,y,z,使得x>y>z,且
+
≤
成立,则实数a的最大值是
| 1 |
| x-y |
| 1 |
| y-z |
| a |
| z-x |
-4
-4
.分析:由已知,可得出(x-z)(
+
)≤-a,利用基本不等式求出(x-z)(
+
)的最值后,再研究a的最值.
| 1 |
| x-y |
| 1 |
| y-z |
| 1 |
| x-y |
| 1 |
| y-z |
解答:解:x>y>z,且
+
≤
成立,两边同乘以x-z得
(x-z)(
+
)≤-a,而(x-z)(
+
)=[(x-y)+(y-z)](
+
)=2+
+
≥2+2
=4,当且仅当
=
,即x-y=y-z时取得等号.
所以4≤-a,即a≤-4,a的最大值是-4.
故答案为:-4.
| 1 |
| x-y |
| 1 |
| y-z |
| a |
| z-x |
(x-z)(
| 1 |
| x-y |
| 1 |
| y-z |
| 1 |
| x-y |
| 1 |
| y-z |
| 1 |
| x-y |
| 1 |
| y-z |
| y-z |
| x-y |
| x-y |
| y-z |
|
| y-z |
| x-y |
| x-y |
| y-z |
所以4≤-a,即a≤-4,a的最大值是-4.
故答案为:-4.
点评:本题考查参数分离、基本不等式求最值.考查了转化、变形、配凑常数的方法.

练习册系列答案
相关题目
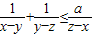 成立,则实数a的最大值是 .
成立,则实数a的最大值是 .