Question

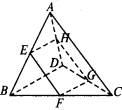
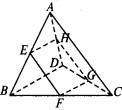
已知：如图，空间四边形ABCD中，E、H分别为BC、AB的中点，F在CD上，G在AD上，且有DF∶FC＝DG∶GA＝2∶3，求证：直线EF、BD、HG交于一点．

Answer 1

[解析]　连结EH、AC、FG.

∵E、H分别为BC、AB的中点，

∴EH綊AC，

∵DF∶FC＝2∶3，DG∶GA＝2∶3，

∴FG∥AC，FG＝AC，∴EH∥FG且FH≠FG，

∴E、F、G、H四点共面且EF与GH不平行．

∴EF与GH相交．

设EF∩GH＝O，则O∈GH，O∈EF，

∵GH⊂平面ABD，EF⊂平面BCD，

∴O∈平面ABD，O∈平面BCD.

∴平面ABD∩平面BCD＝BD，∴O∈BD，

∴即直线EF、BD、HG交于一点．