题目内容
已知函数f(x)=log3x.
(Ⅰ)若关于x的方程f(ax)•f(ax2)=f(3)的解都在区间(0,1)内,求实数a的范围;
(Ⅱ)若函数f(x2-2ax+3)在区间[2,+∞)上单调递增,求正实数a的取值范围.
解:(Ⅰ)∵f(ax)f(ax2)=f(3),∴log3ax• =log33,
=log33,
∴(log3a+log3x)(log3a+2log3x)=1,∴2(log3x)2+3log3a•log3x+log32a-1=0.
令t=log3x,∵0<x<1,∴t<0.∴方程2t2+3log3a•t+log32a-1=0的两根为负.
∴△=(3log3a)2-8(log32a-1)≥0,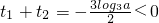 ,
,
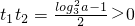 ,∴
,∴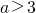 .…(7分)
.…(7分)
(Ⅱ)∵函数f(x2-2ax+3)=log3(x2-2ax+3)在[2,+∞)上单调递增,
∴g(x)=x2-2ax+3在[2,+∞)上大于零且单调递增,
 ,∴
,∴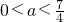 .…(12分)
.…(12分)
分析:(Ⅰ)由条件可得2(log3x)2+3log3a•log3x+log32a-1=0,令t=log3x,可得方程2t2+3log3a•t+log32a-1=0的
两根为负,由判别式大于或等于0及两根之和小于0、两根之积大于0,求出实数a的范围.
(Ⅱ)由题意可得g(x)=x2-2ax+3在[2,+∞)上大于零且单调递增, ,由此求得正实数a的取值范围.
,由此求得正实数a的取值范围.
点评:本题主要考查一元二次方程的根的分布与系数的关系,复合函数的单调性的判断和证明,换元过程中注意变量范围
的改变.
 =log33,
=log33,∴(log3a+log3x)(log3a+2log3x)=1,∴2(log3x)2+3log3a•log3x+log32a-1=0.
令t=log3x,∵0<x<1,∴t<0.∴方程2t2+3log3a•t+log32a-1=0的两根为负.
∴△=(3log3a)2-8(log32a-1)≥0,
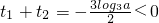 ,
,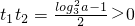 ,∴
,∴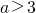 .…(7分)
.…(7分)(Ⅱ)∵函数f(x2-2ax+3)=log3(x2-2ax+3)在[2,+∞)上单调递增,
∴g(x)=x2-2ax+3在[2,+∞)上大于零且单调递增,
 ,∴
,∴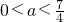 .…(12分)
.…(12分)分析:(Ⅰ)由条件可得2(log3x)2+3log3a•log3x+log32a-1=0,令t=log3x,可得方程2t2+3log3a•t+log32a-1=0的
两根为负,由判别式大于或等于0及两根之和小于0、两根之积大于0,求出实数a的范围.
(Ⅱ)由题意可得g(x)=x2-2ax+3在[2,+∞)上大于零且单调递增,
 ,由此求得正实数a的取值范围.
,由此求得正实数a的取值范围.点评:本题主要考查一元二次方程的根的分布与系数的关系,复合函数的单调性的判断和证明,换元过程中注意变量范围
的改变.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目