题目内容
已知四边形ABCD是等腰梯形,AB=3,DC=1,∠BAD=45°,DE⊥AB(如图1)。现将△ADE沿DE折起,使得AE⊥EB(如图2),连结AC,AB,设M是AB的中点。
(I)求证:BC⊥平面AEC;
(II)判断直线EM是否平行于平面ACD,并说明理由.

证:(I)在图1中,过C作CF⊥EB,

∵DE⊥EB,∴四边形CDEF是矩形,
∵CD=1,∴EF=1。
∵四边形ABCD是等腰梯形,AB=3。
∴AE=BF=1。
∵∠BAD=45°,∴DE=CF=1。
连结CE,则CE=CB=![]()
∵EB=2,∴∠BCE=90°。
则BC⊥CE。
在图2中,∵AE⊥EB,AE⊥ED,EB∩ED=E,
∴AE⊥平面BCDE。
∵BC![]() 平面BCDE,∴AE⊥BC。
平面BCDE,∴AE⊥BC。
∵AE∩CE=E,∴BC⊥平面AEC。
(II)用反证法。
假设EM∥平面ACD。
∵EB∥CD,CD![]() 平面ACD,EB
平面ACD,EB![]() 平面ACD,
平面ACD,
∴EB∥平面ACD。∵EB∩EM=E,∴面AEB∥面ACD
而A∈平面AEB,A∈平面ACD,
与平面AEB//平面ACD矛盾。
∵假设不成立。
∴EM与平面ACD不平行。

 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 17、如图,已知四边形ABCD 是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点.
17、如图,已知四边形ABCD 是矩形,PA⊥平面ABCD,M,N分别是AB,PC的中点. 某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2.
某城市计划在如图所示的空地ABCD上竖一块长方形液晶广告屏幕MNEF,宣传该城市未来十年计划、目标等相关政策.已知四边形ABCD是边长为30m的正方形,电源在点P处,点P到边AD、AB的距离分别为9m,3m,且MN~NE=16~9,线段MN必过点P,端点M、N分别在边AD、AB上,设AN=xm,液晶广告屏幕MNEF的面积为Sm2. 如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.
如图,已知四边形ABCD是菱形,PA⊥平面ABCD,PA=AB=BD=2,AC与BD交于E点,F是PD的中点.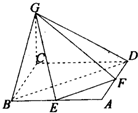 如图:已知四边形ABCD是边长为4的正方形,E、F分别是AB,AD的中点,GC垂直于ABCD所在平面,且GC=2.
如图:已知四边形ABCD是边长为4的正方形,E、F分别是AB,AD的中点,GC垂直于ABCD所在平面,且GC=2. 已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.
已知四边形ABCD是空间四边形,E,F,G,H分别是边AB,BC,CD,DA的中点,求证:四边形EFGH是平行四边形.