题目内容
等差数列 ,
,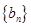 的前
的前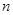 项和分别为
项和分别为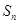 ,
,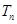 ,若
,若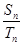 =
=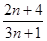 ,则
,则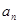 =
=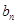 时
时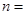 ( )
( )
| A.2 | B.6 | C.无解 | D.无数多个 |
A
解析试题分析:因为 ,所以当
,所以当 时,
时, ,解得
,解得 。故A正确。
。故A正确。
考点:1等差中项;2等差数列的前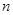 项和。
项和。

练习册系列答案
相关题目
设等差数列 的公差为d,若数列
的公差为d,若数列 为递减数列,则( )
为递减数列,则( )
A. | B. | C. | D. |
已知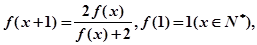 猜想
猜想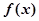 的表达式为( )
的表达式为( )
A.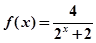 | B.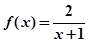 |
C.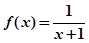 | D.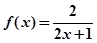 |
设 为等差数列
为等差数列 的前
的前 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( )
A. | B. |
C. | D.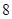 |
数列 …中的
…中的 等于( )
等于( )
A. | B. | C. | D. |
已知 是等比数列,有
是等比数列,有 ,
, 是等差数列,且
是等差数列,且 ,则
,则 ( )
( )
| A.4 | B.8 | C.0或8 | D.16 |
已知等差数列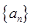 的公差
的公差 ,若
,若 成等比数列,那么公比为( )
成等比数列,那么公比为( )
A. | B. | C. | D. |
已知函数f(x)满足f(x+1)= +f(x),x∈R,且f(1)=
+f(x),x∈R,且f(1)= ,则数列{f(n)}(n∈N*)的前20项的和为( )
,则数列{f(n)}(n∈N*)的前20项的和为( )
| A.305 | B.315 | C.325 | D.335 |
 }中,
}中, =-5,它的前11项的平均值是5,若从中抽取1项,余下10项的平均值是4,则抽取的是( )
=-5,它的前11项的平均值是5,若从中抽取1项,余下10项的平均值是4,则抽取的是( )


