题目内容
已知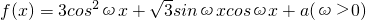 ,且函数f(x)的图象相邻两条对称轴之间的距离为
,且函数f(x)的图象相邻两条对称轴之间的距离为
(1)求ω的值,
(2)若当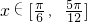 时,f(x)的最小值为2,求a的值,
时,f(x)的最小值为2,求a的值,
(3)求函数f(x)在区间 上的递减区间.
上的递减区间.
解:(1)
= (3+3cos2ωx)+
(3+3cos2ωx)+ sin2ωx+a
sin2ωx+a
= sin(2ωx+
sin(2ωx+ )+a+
)+a+ ,
,
因为函数f(x)的图象相邻两条对称轴之间的距离为 ,
,
所以函数的周期为:π.
所以ω=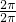 =1,ω的值为1.
=1,ω的值为1.
(2)因为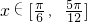 ,所以2x+
,所以2x+ ∈
∈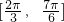 ,
,
∵f(x)的最小值为2,
∴ ,∴a=
,∴a=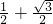 .
.
(3)由(1)可知函数f(x)= sin(2x+
sin(2x+ )+a+
)+a+ ,
,
由2kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,解得
,k∈Z,解得 ,
,
所以在区间 上的递减区间为:
上的递减区间为: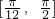 .
.
分析:(1)通过二倍角公式以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过函数的周期求出ω的值,
(2)通过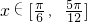 ,求出相位的范围,利用f(x)的最小值为2,即可求a的值,
,求出相位的范围,利用f(x)的最小值为2,即可求a的值,
(3)通过函数的解析式,利用正弦函数的单调减区间求出函数f(x)在区间 上的递减区间.
上的递减区间.
点评:本题考查二倍角公式的应用,两角和的正弦函数,正弦函数的单调性,考查计算能力.

=
 (3+3cos2ωx)+
(3+3cos2ωx)+ sin2ωx+a
sin2ωx+a=
 sin(2ωx+
sin(2ωx+ )+a+
)+a+ ,
,因为函数f(x)的图象相邻两条对称轴之间的距离为
 ,
,所以函数的周期为:π.
所以ω=
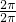 =1,ω的值为1.
=1,ω的值为1.(2)因为
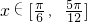 ,所以2x+
,所以2x+ ∈
∈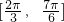 ,
,∵f(x)的最小值为2,
∴
 ,∴a=
,∴a=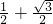 .
.(3)由(1)可知函数f(x)=
 sin(2x+
sin(2x+ )+a+
)+a+ ,
,由2kπ+
 ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ ,k∈Z,解得
,k∈Z,解得 ,
,所以在区间
 上的递减区间为:
上的递减区间为: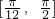 .
.分析:(1)通过二倍角公式以及两角和的正弦函数,化简函数为一个角的一个三角函数的形式,通过函数的周期求出ω的值,
(2)通过
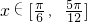 ,求出相位的范围,利用f(x)的最小值为2,即可求a的值,
,求出相位的范围,利用f(x)的最小值为2,即可求a的值,(3)通过函数的解析式,利用正弦函数的单调减区间求出函数f(x)在区间
 上的递减区间.
上的递减区间.点评:本题考查二倍角公式的应用,两角和的正弦函数,正弦函数的单调性,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,且函数f(x)的图象相邻两条对称轴之间的距离为
,且函数f(x)的图象相邻两条对称轴之间的距离为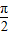
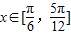 时,f(x)的最小值为2,求a的值,
时,f(x)的最小值为2,求a的值,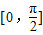 上的递减区间.
上的递减区间.