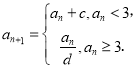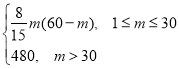题目内容
【题目】已知函数![]() ,
,![]() ,(常数
,(常数![]() 且
且![]() ).
).
(Ⅰ)当![]() 与
与![]() 的图象相切时,求
的图象相切时,求![]() 的值;
的值;
(Ⅱ)设![]() ,若
,若![]() 存在极值,求
存在极值,求![]() 的取值范围.
的取值范围.
【答案】(I) ![]() (Ⅱ)
(Ⅱ) ![]()
【解析】
(Ⅰ)设切点为![]() ,再利用导数的几何意义求出a的值;(Ⅱ)由题得
,再利用导数的几何意义求出a的值;(Ⅱ)由题得![]() ,再对a分类讨论,利用导数分析函数极值情况得到
,再对a分类讨论,利用导数分析函数极值情况得到![]() 的取值范围.
的取值范围.
解:(Ⅰ)设切点为![]() ,
,![]() ,
,
所以过![]() 点的切线方程为
点的切线方程为![]() ,即
,即![]() ,
,
所以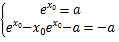 ,解得
,解得![]() .
.
(Ⅱ)依题意,![]() ,
,![]() ,
,
当a>0时,令![]() ,则
,则![]() ,
,
令![]() ,
,![]() ,令
,令![]() ,
,![]() ,
,
所以,当![]() 时,
时,![]() 单调递减;当
单调递减;当![]() 时,
时,![]() 单调递增.
单调递增.
若![]() 存在极值,则
存在极值,则![]() ,即
,即![]() ,
,
又![]() 时,
时,![]() ,
,
所以,![]() 时,
时,
![]() 在
在![]() 存在零点
存在零点![]() ,且在
,且在![]() 左侧
左侧![]() ,在
,在![]() 右侧
右侧![]() ,
,
即![]() 存在变号零点.
存在变号零点.
当a<0时,当![]() 时,
时,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() 单调递减.
单调递减.
若![]() 存在极值,则
存在极值,则![]() ,即
,即![]() ,
,
又![]() 时,
时,![]() ,
,
所以,![]() 时,
时,
![]() 在
在![]() 存在零点
存在零点![]() ,且在
,且在![]() 左侧
左侧![]() ,在
,在![]() 右侧
右侧![]() ,
,
即![]() 存在变号零点.
存在变号零点.
所以,若![]() 存在极值,
存在极值,![]() .
.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目