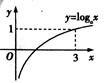
题目内容
设函数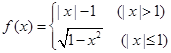 关于
关于 的方程
的方程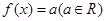 的解的个数不可能是( )
的解的个数不可能是( )
| A.1 | B.2 | C.3 | D.4 |
A
解析试题分析:可以先分别画出函数 与
与 的图象,然后结合图象的特征即可获得解答.
的图象,然后结合图象的特征即可获得解答.
考点:根的存在性及根的个数判断.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知定义在R上的函数 满足条件
满足条件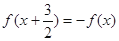 ,且函数
,且函数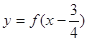 为奇函数,给出以下四个命题①函数
为奇函数,给出以下四个命题①函数 的最小正周期是
的最小正周期是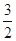 ;②函数
;②函数 的图象关于点
的图象关于点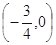 对称;③函数
对称;③函数 为R上的偶函数;④函数
为R上的偶函数;④函数 为R上的单调函数。其中真命题的个数是( )
为R上的单调函数。其中真命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
设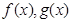 分别是定义在
分别是定义在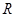 上的奇函数和偶函数,当
上的奇函数和偶函数,当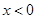 时,
时,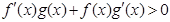 ,
,
且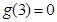 ,则不等式
,则不等式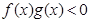 的解集是( )
的解集是( )
A.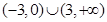 | B.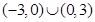 |
C.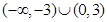 | D.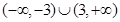 |
若函数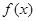 的零点与
的零点与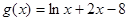 的零点之差的绝对值不超过
的零点之差的绝对值不超过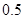 , 则
, 则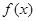 可以是( )
可以是( )
A.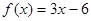 | B.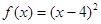 |
C.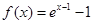 | D.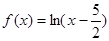 |
函数y=ln( )(x>-1)的反函数是( )
)(x>-1)的反函数是( )
A. | B. |
C. | D. . . |
已知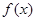 为偶函数,当
为偶函数,当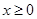 时,
时,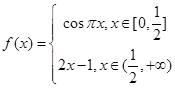 ,则不等式
,则不等式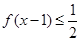 的解集为( )
的解集为( )
A. | B.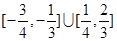 |
C.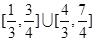 | D.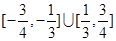 |
已知函数 ,在下列区间中,包含
,在下列区间中,包含 零点的区间是( )
零点的区间是( )
A. | B. | C. | D. |
已知f(x+1)=f(x-1),f(x)=f(-x+2),方程f(x)=0在[0,1]内有且只有一个根x=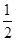 ,则f(x)=0在区间[0,2014]内根的个数为( )
,则f(x)=0在区间[0,2014]内根的个数为( )
| A.1006 | B.1007 | C.2013 | D.2014 |
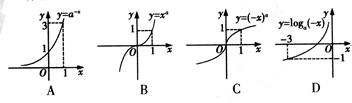
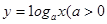 ,且
,且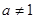 )的图像如右图所示,则下列函数图像正确的是
)的图像如右图所示,则下列函数图像正确的是