题目内容
(理)已知正数列{an}中,对任意的正整数n,都(n+1)an2-anan+12=nan+12成立,且a1=2,则极限| lim |
| n→∞ |
| an |
| 3n+1 |
分析:根据nan+12=(n+1)an2+anan+1,得到
=
,利用累乘法即可求得该数列的通项公式,根据极限的求法即可求得结果.
| an+1 |
| an |
| n+1 |
| n |
解答:解:∵nan+12=(n+1)an2+anan+1
即[(n+1)an-nan+1](an+an+1)=0
∴(n+1)an-nan+1=0 或an+an+1=0
又∵数列{an}各项均为正数
∴
=
,
∴
=
,
=
,
=
…
=
∴
=
,∴an=2n,
∴极限
=
=
即[(n+1)an-nan+1](an+an+1)=0
∴(n+1)an-nan+1=0 或an+an+1=0
又∵数列{an}各项均为正数
∴
| an+1 |
| an |
| n+1 |
| n |
∴
| a2 |
| a1 |
| 2 |
| 1 |
| a3 |
| a2 |
| 3 |
| 2 |
| a4 |
| a3 |
| 4 |
| 3 |
| an |
| an-1 |
| n |
| n-1 |
∴
| an |
| a1 |
| n |
| 1 |
∴极限
| lim |
| n→∞ |
| an |
| 3n+1 |
| lim |
| n→∞ |
| 2n |
| 3n+1 |
| 2 |
| 3 |
点评:本题考查根据递推关系求数列通项公式的方法,对于此种类型的题目首先化简递推式,推导出相邻两项的关系是解题的关键,考查运算能力,属中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
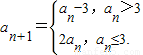
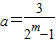 (m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.
(m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.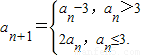
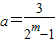 (m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.
(m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.