题目内容
P为椭圆 上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 .
上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 .
【答案】分析:由于分别过焦点且垂直于x轴的直线与椭圆的交点P可构成四个直角三角形.欲使△F1PF2为直角三角形的点P共有8个,由椭圆的几何性质可知,当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,必须∠F1PF2>90°,此时 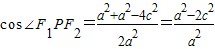 <0,∴
<0,∴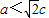 ,由此能够推导出该椭圆的离心率的取值范围.
,由此能够推导出该椭圆的离心率的取值范围.
解答: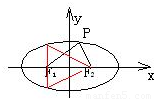 解:由题意可知,分别过焦点且垂直于x轴的直线与椭圆的交点P可构成四个直角三角形.
解:由题意可知,分别过焦点且垂直于x轴的直线与椭圆的交点P可构成四个直角三角形.
而当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,
由条件:欲使△F1PF2为直角三角形的点P共有8个,必须∠F1PF2>90°,
故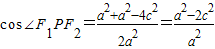 <0,⇒
<0,⇒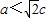 ,
,
∴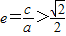 ,
,
又∵0<e<1,∴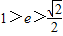 .
.
故答案为: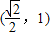 .
.
点评:本题考查椭圆的性质及其应用、余弦定理等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.
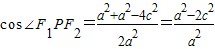 <0,∴
<0,∴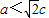 ,由此能够推导出该椭圆的离心率的取值范围.
,由此能够推导出该椭圆的离心率的取值范围.解答:
 解:由题意可知,分别过焦点且垂直于x轴的直线与椭圆的交点P可构成四个直角三角形.
解:由题意可知,分别过焦点且垂直于x轴的直线与椭圆的交点P可构成四个直角三角形.而当点P位于(0,b)或(0,-b)处时,∠F1PF2最大,
由条件:欲使△F1PF2为直角三角形的点P共有8个,必须∠F1PF2>90°,
故
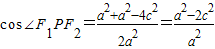 <0,⇒
<0,⇒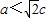 ,
,∴
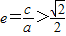 ,
,又∵0<e<1,∴
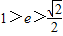 .
.故答案为:
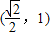 .
.点评:本题考查椭圆的性质及其应用、余弦定理等基础知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.

练习册系列答案
 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目





 上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________;
上一点,F1,F2是椭圆的焦点,∠F1PF2=900,则△F1PF2的面积为___________;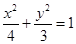 上一点,F1、F2为该椭圆的两个焦点,若
上一点,F1、F2为该椭圆的两个焦点,若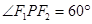 ,则
,则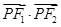 =(
)
=(
)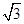 C.
C. D.2
D.2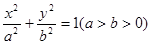 上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 ▲
上一点,F1、F2是椭圆的左、右焦点,若使△F1PF2为直角三角形的点P共有8个,则椭圆离心率的取值范围是 ▲
 上一点,F1、F2为左右焦点,∠F1PF2=90°
上一点,F1、F2为左右焦点,∠F1PF2=90° ;
;