题目内容
设椭圆
=1(a＞b＞0)的离心率为e=
.（1）椭圆的左、右焦点分别为F1、F2,A是椭圆上的一点，且点A到此两焦点的距离之和为4,求椭圆的方程.
（2）求b为何值时，过圆x2+y2=t2上一点M（2，
）处的切线交椭圆于Q1、Q2两点，而且OQ1⊥OQ2?
解:（1）椭圆的方程为+=1.
（2）过圆x2+y2=t2上的一点M（2,）处的切线方程为2x+
y-6=0.
令Q1(x1,y1)，Q2(x2,y2),则
化为5x2－24x+36－2b2=0.由Δ＞0得b＞
,
x1+x2=
,x1x2=
,y1y2=2x1x2-6(x1+x2)+18=
.
由OQ1⊥OQ2,知x1x2+y1y2=0
b2=9,
即b=3∈（
,+∞），故b=3.
练习册系列答案
相关题目
=1(a＞b＞0)的右焦点为F1，右准线为l1,若过点F1且垂直于x轴的弦长等于点F1到准线l1的距离，则椭圆的离心率是_________.
=1(a＞b＞0)的面积为πab,过坐标原点的直线l、x轴的正半轴及椭圆围成的两个区域的面积分别为s、t(如图),则s关于t的函数图象的大致形状为
+
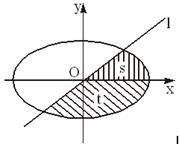
=1(a＞b＞0)的左焦点为F1(－2,0),左准线l1与x轴交于点N(－3,0),过点N且倾斜角为30°的直线l交椭圆于A、B两点.