题目内容
以双曲线 的离心率为首项,以函数
的离心率为首项,以函数 的零点为公比的等比数列的前
的零点为公比的等比数列的前 项的和
项的和
A. | B. |
C. | D. |
B
解析试题分析:双曲线 的离心率
的离心率 =
= ,即等比数列的首项为
,即等比数列的首项为 ;令
;令 =0得,x=
=0得,x= ,即数列的公比,所以等比数列的前
,即数列的公比,所以等比数列的前 项的和
项的和
 ,故选B。
,故选B。
考点:本题主要考查双曲线的几何性质,等比数列的求和公式,零点的概念。
点评:小综合题,拼凑而成,思路明确。涉及双曲线的考题,往往与a,b,c,e有关,特别是其离心率,有不同表达形式。

练习册系列答案
相关题目
已知实数 构成一个等比数列,则圆锥曲线
构成一个等比数列,则圆锥曲线 的离心率为( )
的离心率为( )
A. | B.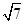 | C. 或 或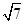 | D. 或7 或7 |
如果椭圆 上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
| A.10 | B.6 | C.12 | D.14 |
已知双曲线 =1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
| A.[1,2] | B.(1,2) | C.[2,+∞) | D.(2,+∞) |
已知椭圆 与曲线
与曲线 的离心率互为倒数,则
的离心率互为倒数,则 ( )
( )
| A.16 | B. | C. | D. |
已知有相同两焦点 的椭圆
的椭圆 和双曲线
和双曲线 ,
, 是它们的一个交点,则
是它们的一个交点,则 的形状是 ( )
的形状是 ( )
| A.锐角三角形 | B.直角三角形 | C.钝有三角形 | D.等腰三角形 |
已知焦点在 轴上的椭圆
轴上的椭圆 的离心率是
的离心率是 ,则
,则 的值为 ( )
的值为 ( )
A.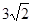 | B. | C. | D. |
 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )



 :抛物线
:抛物线 的准线方程为
的准线方程为 ;命题
;命题 :平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )
:平面内两条直线的斜率相等是两条直线平行的充分不必要条件;则下列命题是真命题的是( )


