ЬтФПФкШн
ЁОЬтФПЁПШчЭМ1ЫљЪОЮЊвЛжжФЇЖЙЕѕЕЦЃЌЭМ2ЮЊИУЕѕЕЦЕФПђМмНсЙЙЭМЃЌгЩе§СљРтзЖ![]() КЭ
КЭ![]() ЙЙГЩЃЌСНИіРтзЖЕФВрРтГЄОљЯрЕШЃЌЧвРтзЖЕзУцЭтНгдВЕФжБОЖЮЊ
ЙЙГЩЃЌСНИіРтзЖЕФВрРтГЄОљЯрЕШЃЌЧвРтзЖЕзУцЭтНгдВЕФжБОЖЮЊ![]() ЃЌЕзУцжааФЮЊ
ЃЌЕзУцжааФЮЊ![]() ЃЌЭЈЙ§СЌНгЯпМАЮќХЬЙЬЖЈдкЬьЛЈАхЩЯЃЌЪЙРтзЖЕФЕзУцГЪЫЎЦНзДЬЌЃЌЯТЖЅЕу
ЃЌЭЈЙ§СЌНгЯпМАЮќХЬЙЬЖЈдкЬьЛЈАхЩЯЃЌЪЙРтзЖЕФЕзУцГЪЫЎЦНзДЬЌЃЌЯТЖЅЕу![]() гыЬьЛЈАхЕФОрРыЮЊ
гыЬьЛЈАхЕФОрРыЮЊ![]() ЃЌЫљгаЕФСЌНгЯпЖМгУЬиЪтЕФН№ЪєЬѕжЦГЩЃЌЩшН№ЪєЬѕЕФзмГЄЮЊyЃЎ
ЃЌЫљгаЕФСЌНгЯпЖМгУЬиЪтЕФН№ЪєЬѕжЦГЩЃЌЩшН№ЪєЬѕЕФзмГЄЮЊyЃЎ
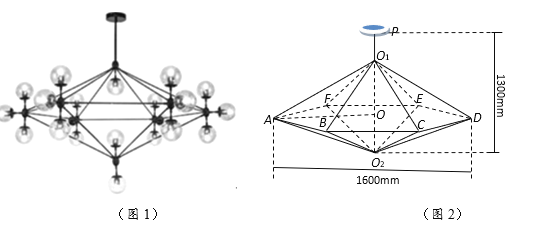
ЃЈ1ЃЉЩшЁЯO1AO =![]() (rad)ЃЌНЋyБэЪОГЩІШЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіІШЕФЗЖЮЇЃЛ
(rad)ЃЌНЋyБэЪОГЩІШЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіІШЕФЗЖЮЇЃЛ![]()
ЃЈ2ЃЉЧыФуЩшМЦІШЃЌЕБНЧІШе§ЯвжЕЕФДѓаЁЪЧЖрЩйЪБЃЌН№ЪєЬѕзмГЄyзюаЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎЃЈ2ЃЉЕБНЧ
ЃЉЃЎЃЈ2ЃЉЕБНЧ![]() Тњзу
Тњзу![]() ЃЈ
ЃЈ![]() ЃЉЪБЃЌН№ЪєЬѕзмГЄyзюаЁЃЎ
ЃЉЪБЃЌН№ЪєЬѕзмГЄyзюаЁЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉдкжБНЧШ§НЧаЮOAO1жаЃЌРћгУШ§НЧКЏЪ§ЕФЖЈвхЃЌгУ![]() БэЪО
БэЪО![]() ЃЌЦфжагЩЪЕМЪЮЪЬтПЩЕУІШЕФЗЖЮЇЃЌзюКѓАбЕѕЕЦ12ЬѕВрРтЃЌ6ЬѕЕзБпЃЌ1ЬѕЖЅаќГЄЯрМгБэЪОyЃЌЕУД№АИЃЛ
ЃЌЦфжагЩЪЕМЪЮЪЬтПЩЕУІШЕФЗЖЮЇЃЌзюКѓАбЕѕЕЦ12ЬѕВрРтЃЌ6ЬѕЕзБпЃЌ1ЬѕЖЅаќГЄЯрМгБэЪОyЃЌЕУД№АИЃЛ
ЃЈ2ЃЉЮЊСЫЗНБудЫЫуЃЌжЛСю![]() ЃЌРћгУЧѓЕМЕФЗНЪНЕУМЋжЕЃЌДЫЪБМДЮЊзюаЁжЕ.
ЃЌРћгУЧѓЕМЕФЗНЪНЕУМЋжЕЃЌДЫЪБМДЮЊзюаЁжЕ.
ЃЈ1ЃЉдкжБНЧШ§НЧаЮOAO1жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
ЫљвдІШЕФЗЖЮЇЪЧ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ДгЖјга![]()
![]()
![]() ЃЌ
ЃЌ
Ыљвд![]() ЃЌ
ЃЌ![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ2ЃЉСю![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌ
ЃЌ
Сю![]() ЃЌдђ
ЃЌдђ![]() ЃЌдђ
ЃЌдђ![]() ЃЎ
ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЎ
ЃЎ
КЏЪ§![]() ЕФЕЅЕїадгы
ЕФЕЅЕїадгы![]() ЙиЯЕСаБэШчЯТЃК
ЙиЯЕСаБэШчЯТЃК
|
|
|
|
|
| 0 | + |
|
| МЋаЁжЕ |
|
ЫљвдЕБ![]() ЃЌЦфжа
ЃЌЦфжа![]() ЪБ
ЪБ![]() ШЁЕУзюаЁжЕЃЌМДyзюаЁЃЎ
ШЁЕУзюаЁжЕЃЌМДyзюаЁЃЎ
ЙЪЕБНЧ![]() Тњзу
Тњзу![]() ЃЈ
ЃЈ![]() ЃЉЪБЃЌН№ЪєЬѕзмГЄyзюаЁЃЎ
ЃЉЪБЃЌН№ЪєЬѕзмГЄyзюаЁЃЎ